
| 2S |
| l |
| 3V |
| S |
| ||
| 2 |
| ||
| 3 |
| 3V |
| S |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3V |
| S |
| a2+b2+c2 |
| ||
| 2 |
| ||
| 3 |


科目:高中数学 来源: 题型:
| 2S |
| l |
| 3V |
| S |
| ||
| 2 |
| ||
| 3 |
| A、两人都对 | B、甲错、乙对 |
| C、甲对、乙错 | D、两人都错 |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三下学期数学单元测试3-文科 题型:选择题
学习合情推理后,甲、乙两位同学各举了一个例子,甲:由“若三角形周长为 ,面积为S,则其内切圆半径
,面积为S,则其内切圆半径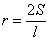 ”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径
”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径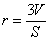 ”;乙:由“若直角三角形两直角边长分别为
”;乙:由“若直角三角形两直角边长分别为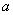 ,b,则其外接圆半径
,b,则其外接圆半径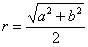 ”;类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为
”;类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为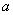 、b、c,则其外接球半径
、b、c,则其外接球半径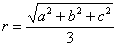 ”.这两位同学类比得出的结论 ( )
”.这两位同学类比得出的结论 ( )
A.两人都对 B.甲错、乙对 C.甲对、乙错 D.两人都错
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 2S |
| l |
| 3V |
| S |
| ||
| 2 |
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源:2011年河南省郑州四中高三数学一轮复习综合测试(3)(解析版) 题型:选择题
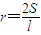 ”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径
”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径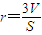 ”;乙:由“若直角三角形两直角边长分别为a,b,则其外接圆半径
”;乙:由“若直角三角形两直角边长分别为a,b,则其外接圆半径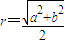 ”;类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为a、b、c,则其外接球半径
”;类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为a、b、c,则其外接球半径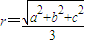 ”.这两位同学类比得出的结论( )
”.这两位同学类比得出的结论( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com