
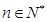 ,
,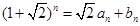 (
(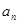 、
、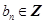 )。
)。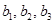 的值;
的值;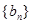 的各项均为奇数.
的各项均为奇数. ,
, ,
, ;(2)见解析.
;(2)见解析. ,得
,得 ,而
,而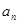 、
、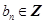
 类似可得,
类似可得, ,
,
 时,易知
时,易知 ,为奇数;
,为奇数;  时,
时, ,其中
,其中 为奇数;
为奇数;  时,
时,

 ,
, ,得
,得 ,而
,而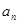 、
、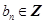
 ,………………………2分
,………………………2分 ,
, …………………………5分
…………………………5分 时,易知
时,易知 ,为奇数;……………………7分
,为奇数;……………………7分 时,
时, ,其中
,其中 为奇数;……………………8分
为奇数;……………………8分 时,
时,
 ,
, , ……………………11分
, ……………………11分 、
、 ,所以
,所以 是偶数,
是偶数, 是奇数,故
是奇数,故 也是奇数. ……………………14分
也是奇数. ……………………14分 的值一定是奇数. -----------------------------15分
的值一定是奇数. -----------------------------15分

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com