
【题目】已知函数![]()
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,求证:
,求证:![]() ;
;
【答案】(1)单调递增区间为![]() .(2)见解析
.(2)见解析
【解析】
(1)根据题意由函数的解析式求出函数的导数,则 ,令
,令![]() ,求出
,求出![]() 的导数,分析
的导数,分析![]() 在
在![]() 的最小值,分析可得
的最小值,分析可得![]() ,由函数的单调性与函数导数的关系,分析可得答案;
,由函数的单调性与函数导数的关系,分析可得答案;
(2)根据题意,原问题可以转化为![]() ,设
,设![]() ,分析可得只须证
,分析可得只须证![]() 成立,求出函数
成立,求出函数![]() 的导数,结合函数的导数与函数单调性的关系,分析可得
的导数,结合函数的导数与函数单调性的关系,分析可得![]() 的最小值,证明其最小值大于0即可得答案.
的最小值,证明其最小值大于0即可得答案.
(1)因为![]() ,
,![]()
令![]() ,则
,则![]() .
.
令![]() ,得
,得![]() (依题意
(依题意![]() ),
),
由![]() ,得
,得 ;由
;由![]() ,得
,得![]() .
.
所以![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间 上单调递增,
上单调递增,
所以![]()
因为![]() ,所以
,所以![]() .
.
所以![]() ,即
,即![]()
所以函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)由![]() ,等价于
,等价于![]() ,
,
等价于![]()
设![]() ,只须证
,只须证![]() 成立.
成立.
因为![]()
由![]() ,得
,得![]() 有异号两根.
有异号两根.
令其正根为![]() ,则
,则![]() .
.
在![]() 上
上![]() ,在
,在![]() 上
上![]() ,
,
则![]() 的最小值为
的最小值为![]()
![]() ,
,
![]() ,所以
,所以![]()
则![]() ,因此
,因此![]() ,
,
即![]() ,所以
,所以![]()
所以![]()


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.回归直线![]() 至少经过其样本数据
至少经过其样本数据![]() 中的一个点
中的一个点
B.从独立性检验可知有99%的把握认为吃地沟油与患胃肠癌有关系时,我们就说如果某人吃地沟油,那么他有99%可能患胃肠癌
C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D.将一组数据的每一个数据都加上或减去同一个常数后,其方差也要加上或减去这个常数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,其中茎为十位数,叶为个位数,甲、乙两人得分的中位数为X甲、X乙,则下列判断正确的是( )
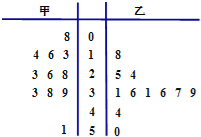
A. X乙﹣X甲=5,甲比乙得分稳定
B. X乙﹣X甲=5,乙比甲得分稳定
C. X乙﹣X甲=10,甲比乙得分稳定
D. X乙﹣X甲=10,乙比甲得分稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高一学年结束后,要对某班的50名学生进行文理分班,为了解数学对学生选择文理科是否有影响,有人对该班的分科情况做了如下的数据统计:
理科人数 | 文科人数 | 总计 | |
数学成绩好的人数 | 25 | 30 | |
数学成绩差的人数 | 10 | ||
合计 | 15 |
(Ⅰ)根据数据关系,完成![]() 列联表;
列联表;
(Ⅱ)通过计算判断能否在犯错误的概率不超过![]() 的前提下认为数学对学生选择文理科有影响.
的前提下认为数学对学生选择文理科有影响.
附:![]()
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把某校![]() 名学生的一次考试成绩(单位:分)分成5组得到的频率分布直方图如图所示,其中落在
名学生的一次考试成绩(单位:分)分成5组得到的频率分布直方图如图所示,其中落在![]() 内的频数为180.
内的频数为180.

(1)请根据图中所给数据,求出本次考试成绩的中位数(保留一位小数);
(2)从这5组中按分层抽样的方法选取40名学生的成绩作为一个样本,在![]() 与
与![]() 内的样本中,再随机抽取两名学生的成绩,求所抽取两名学生成绩的平均分不低于70分的概率.
内的样本中,再随机抽取两名学生的成绩,求所抽取两名学生成绩的平均分不低于70分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取![]() 名同学(男
名同学(男![]() 女
女![]() ),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
几何题 | 代数题 | 总计 | |
男同学 |
|
|
|
女同学 |
|
|
|
总计 |
|
|
|
(1)能否据此判断有![]() 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在![]() 分钟,乙每次解答一道几何题所用的时间在
分钟,乙每次解答一道几何题所用的时间在![]() 分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
(3)现从选择做几何的![]() 名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为
名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为![]() 元,当用水超过4吨时,超过部分每吨为
元,当用水超过4吨时,超过部分每吨为![]() 元,每月甲、乙两户共交水费
元,每月甲、乙两户共交水费![]() 元,已知甲、乙两户该月用水量分别为
元,已知甲、乙两户该月用水量分别为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若甲、乙两户该月共交水费![]() 元,分别求出甲、乙两户该月的用水量.
元,分别求出甲、乙两户该月的用水量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com