
【题目】如图,三棱柱![]() 的侧棱
的侧棱![]() 垂直于底面
垂直于底面![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.

(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由侧棱![]() 垂直于底面
垂直于底面![]() ,且
,且![]() ,得可侧面与底面垂直,从而
,得可侧面与底面垂直,从而![]() 与侧面
与侧面![]() 垂直,因此有
垂直,因此有![]() ,即有
,即有![]() ,于是只要证
,于是只要证![]() 即可有线面垂直,从而证
即可有线面垂直,从而证![]() ,这个
,这个![]() 在矩形
在矩形![]() 由相似三角形可得证;
由相似三角形可得证;
(2)以分别以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,求出平面
轴建立空间直角坐标系,求出平面![]() 和平面
和平面![]() 法向量,有平面法向量夹角的余弦值得二面角的余弦值(注意确定二面角是锐角还是钝角).
法向量,有平面法向量夹角的余弦值得二面角的余弦值(注意确定二面角是锐角还是钝角).
(1)证明:∵![]() 平面
平面![]()
∴四边形![]() 是矩形
是矩形
∵![]() 为
为![]() 中点,且
中点,且![]()
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]() ,∴
,∴![]()
连接![]() ,
,
∵![]() ,∴
,∴![]() 与
与![]() 相似
相似
∴![]() ,∴
,∴![]()
∴![]()
∵![]() ,∴
,∴![]() 平面
平面![]()
∴![]() 平面
平面![]()
∵![]() 平面
平面![]() ,∴
,∴![]()
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
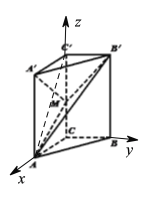
(2)解∶如图,分别以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则
![]() ,
,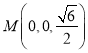 ,
,![]() ,
,![]() ,
,
∴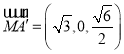 ,
,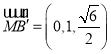 ,
,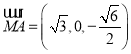 ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,
,![]()
解得: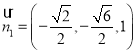
同理,平面![]() 的法向量
的法向量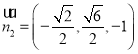
设二面角![]() 的大小为
的大小为![]() ,则
,则
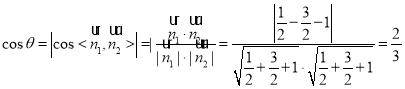
即二面角![]() 的余弦值为
的余弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最,编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”,见证着人民军队迈向世界一流军队的坚定步伐.此次大阅兵不仅得到了全中国人的关注,还得到了无数外国人的关注.某单位有10位外国人,其中关注此次大阅兵的有8位,若从这10位外国人中任意选取3位做一次采访,则被采访者中至少有2位关注此次大阅兵的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Tn为数列{an}的前n项的积,即Tn=a1a2…an.
(1)若Tn=n2,求数列{an}的通项公式;
(2)若数列{an}满足Tn=![]() (1﹣an)(n∈N*),证明数列
(1﹣an)(n∈N*),证明数列![]() 为等差数列,并求{an}的通项公式;
为等差数列,并求{an}的通项公式;
(3)数列{an}共有100项,且满足以下条件:
①![]() ;
;
②![]() (1≤k≤99,k∈N*).
(1≤k≤99,k∈N*).
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试问符合条件的数列共有多少个?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 在线段
在线段![]() 上运动,则 ( )
上运动,则 ( )
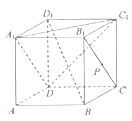
A.直线![]() 平面
平面![]()
B.三棱锥![]() 的体积为定值
的体积为定值
C.异面直线![]() 与
与![]() 所成角的取值范围是
所成角的取值范围是![]()
D.直线![]() 与平面
与平面![]() 所成角的正弦值的最大值为
所成角的正弦值的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过抛物线![]() 焦点
焦点![]() 的直线与抛物线交于
的直线与抛物线交于![]() (其中
(其中![]() 点在
点在![]() 轴的上方)两点.
轴的上方)两点.
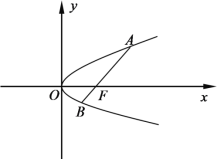
(1)若线段![]() 的长为3,求
的长为3,求![]() 到直线
到直线![]() 的距离;
的距离;
(2)证明:![]() 为钝角三角形;
为钝角三角形;
(3)已知![]() 且
且![]() ,求三角形
,求三角形![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在半径为![]() 的球内有一内接正三棱锥,它的底面三个顶点恰好都在同一个大圆上,一个动点从三棱锥的一个顶点出发沿球面运动,经过其余三点后返回,则经过的最短路程是________
的球内有一内接正三棱锥,它的底面三个顶点恰好都在同一个大圆上,一个动点从三棱锥的一个顶点出发沿球面运动,经过其余三点后返回,则经过的最短路程是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园草坪上有一扇形小径(如图),扇形半径为![]() ,中心角为
,中心角为![]() ,甲由扇形中心
,甲由扇形中心![]() 出发沿
出发沿![]() 以每秒2米的速度向
以每秒2米的速度向![]() 快走,同时乙从
快走,同时乙从![]() 出发,沿扇形弧以每秒
出发,沿扇形弧以每秒![]() 米的速度向
米的速度向![]() 慢跑,记
慢跑,记![]() 秒时甲、乙两人所在位置分别为
秒时甲、乙两人所在位置分别为![]() ,
,![]() ,通过计算
,通过计算![]() ,判断下列说法是否正确:
,判断下列说法是否正确:
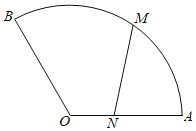
(1)当![]() 时,函数
时,函数![]() 取最小值;
取最小值;
(2)函数![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(3)若![]() 最小,则
最小,则![]() ;
;
(4)![]() 在
在![]() 上至少有两个零点;
上至少有两个零点;
其中正确的判断序号是______(把你认为正确的判断序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为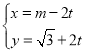 (
(![]() ,
,![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为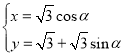 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,求曲线
轴正半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若![]() ,点
,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com