
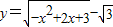 (x∈[0,2])的图象绕坐标原点逆时针旋转θ(θ为锐角),若所得曲线仍是一个函数的图象,则θ的最大值为 .
(x∈[0,2])的图象绕坐标原点逆时针旋转θ(θ为锐角),若所得曲线仍是一个函数的图象,则θ的最大值为 . 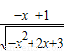 ,再设函数在 x=0 处,函数图象的切线斜率为k,则k=f'(0)=
,再设函数在 x=0 处,函数图象的切线斜率为k,则k=f'(0)=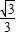 =tan30°,可得切线的倾斜角为 30°.因此,可得要使旋转后的图象仍为一个函数的图象,最大旋转角为 90°-30°=60°.
=tan30°,可得切线的倾斜角为 30°.因此,可得要使旋转后的图象仍为一个函数的图象,最大旋转角为 90°-30°=60°.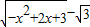 ,根据二次函数的单调性,可得
,根据二次函数的单调性,可得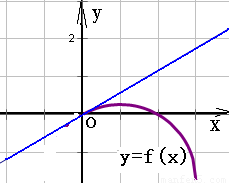 函数在[0,1]上为增函数,在[1,2]上为减函数.
函数在[0,1]上为增函数,在[1,2]上为减函数.
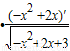 =
=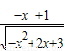 ,
,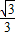 =tan30°,可得切线的倾斜角为 30°,
=tan30°,可得切线的倾斜角为 30°,

科目:高中数学 来源:2012-2013学年浙江省某三县高三(上)期中数学试卷(解析版) 题型:选择题
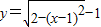 (x∈[0,2])图象绕原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则a的最大值是( )
(x∈[0,2])图象绕原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则a的最大值是( )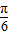
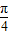
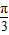
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省湖州市三县高三(上)期中数学试卷(理科)(解析版) 题型:选择题
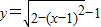 (x∈[0,2])图象绕原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则a的最大值是( )
(x∈[0,2])图象绕原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则a的最大值是( )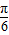
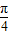
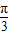
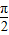
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省某三县高三(上)期中数学试卷(解析版) 题型:选择题
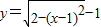 (x∈[0,2])图象绕原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则a的最大值是( )
(x∈[0,2])图象绕原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则a的最大值是( )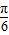
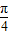
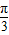
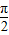
查看答案和解析>>
科目:高中数学 来源:2012年江苏省苏锡常镇四市高考数学一模试卷(解析版) 题型:解答题
 (x∈[0,2])的图象绕坐标原点逆时针旋转θ(θ为锐角),若所得曲线仍是一个函数的图象,则θ的最大值为 .
(x∈[0,2])的图象绕坐标原点逆时针旋转θ(θ为锐角),若所得曲线仍是一个函数的图象,则θ的最大值为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com