练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．如图是某学校一名篮球运动员在10场比赛中所得分数的茎叶图，则该运动员在这10场比赛中得分的中位数为15．

    分析 根据中位数的定义进行求解即可．

    解答 解：根据茎叶图将数据从小到大排列之后，对应的第5个数为14，第6个数为16，
    则对应的中位数为$\frac{14+16}{2}$=15，
    故答案为：15．

    点评 本题主要考查茎叶图的应用以及中位数的求解，利用中位数的定义是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    10．在平面直角坐标系xoy中，己知圆C1：（x+3）2+（y-1）2=25和圆C2：（x-4）2+（y-2）2=4．
    （1）判断两圆的位置关系：
    （2）求过两圆的圆心的直线的方程：
    （3）若直线m过圆C1的圆心，且被圆C2截得的弦长为2$\sqrt{3}$，求直线m的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知△ABC的面积为3，且满足2$\sqrt{3}$≤$\overrightarrow{AB}$•$\overrightarrow{AC}$≤6，设$\overrightarrow{AB}$、$\overrightarrow{AC}$的夹角为θ．
    （1）求θ的取值范围；
    （2）求函数f（θ）=2sin2（$\frac{π}{4}$+θ）-cos2θ的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

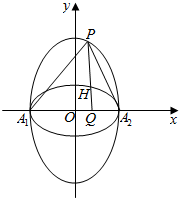    1．若两个椭圆的离心率相等，则称它们为“相似椭圆”．如图，在直角坐标系xOy中，已知椭圆C1：$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1，A1，A2分别为椭圆C1的左右顶点，椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”
    （1）求椭圆C2的方程；
    （2）设P为椭圆C2上异于A1，A2的任意一点，过P作PQ⊥x轴，垂足为Q，线段PQ交椭圆C1于H，求证：H为△PA1A2的垂心（垂心为三角形三条高的交点）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

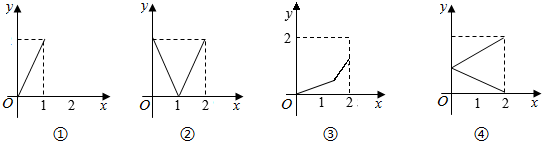
    8．设集合M={x|0≤x≤2}，N={y|0≤y≤2}，从M到N有四种对应如图所示，其中能表示为M到N的函数关系的是（　　）
    A．①②B．②③C．③④D．①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．等比数列{an}的前4项和为4，前12项和为28，则它的前8项和是（　　）
    A．-8B．12C．-8或12D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．平面向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$两两所成角相等，且|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，|$\overrightarrow{c}$|=3，则|$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$|为$\sqrt{3}$或6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足：|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=1，|$\overrightarrow{a}$-2$\overrightarrow{b}$|≤2，则$\overrightarrow{b}$在$\overrightarrow{a}$上的投影长度的取值范围是（　　）
    A．[0，$\frac{1}{13}$]B．（0，$\frac{5}{13}$]C．[$\frac{1}{13}$，1]D．[$\frac{3}{4}$，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知直角三角形的两直角边长分别为2和4，求两直角边上的中线所夹的锐角的余弦值．

    查看答案和解析>>

    同步练习册答案