
【题目】某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由形状为长方形A1B1C1D1的休闲区和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米(如图所示).

(1)若设休闲区的长和宽的比![]() =x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
=x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,则休闲区A1B1C1D1的长和宽该如何设计?
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1. 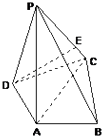
(1)求二面角A﹣PB﹣C的余弦值.
(2)在线段CP上是否存在一点E,使得DE⊥PB,若存在,求线段CE的长度,不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,方程f(x)=0有3个不同的根.
,方程f(x)=0有3个不同的根.
(1)求实数m的取值范围;
(2)是否存在实数m,使得f(x)在(0,1)上恰有两个极值点x1 , x2且满足x2=2x1 , 若存在,求实数m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点
的一个焦点![]() 与抛物线
与抛物线![]() 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为![]() .
.
(1)求该椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且点
两点,且点![]() 恰为弦
恰为弦![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据条件,求下列曲线的方程.
(1)已知两定点![]() ,曲线上的点
,曲线上的点![]() 到
到![]() 距离之差的绝对值为
距离之差的绝对值为![]() ,求曲线的方程;
,求曲线的方程;
(2)在 ![]() 轴上的一个焦点与短轴两端点的连线互相垂直,且焦距为
轴上的一个焦点与短轴两端点的连线互相垂直,且焦距为![]() 的椭圆的标准方程.
的椭圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且S2=11,S5=50,则过点P(n,an)和Q(n+2,an+2)(n∈N*)的直线的一个方向向量的坐标可以是( )
A.(﹣1,﹣3)
B.(1,﹣3)
C.(1,1)
D.(1,﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com