
【题目】设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2006(x)=( )
A.sinx
B.﹣sinx
C.cosx
D.﹣cosx
 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,单位圆O与y轴负半轴交于点O',过点O'作与x轴平行的直线AB,射线O'P从O'A出发,绕着点O'逆时针方向旋转至O'B,在旋转的过程中,记∠AO'P=x(0<x<π),O'P所经过的在单位圆O内区域(阴影部分)的面积为S.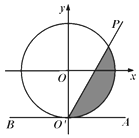
(1)如果 ![]() ,那么S=;
,那么S=;
(2)关于函数S=f(x)的以下两个结论:
①对任意 ![]() ,都有
,都有 ![]() ;
;
②对任意x1 , x2∈(0,π),且x1≠x2 , 都有 ![]() .
.
其中正确的结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的左焦点为F1 , 右焦点为F2 . 若椭圆上存在一点P,满足线段PF2相切于以椭圆的短轴为直径的圆,切点为线段PF2的中点,则该椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程 ![]() ﹣
﹣ ![]() =1表示焦点在y轴上的椭圆;命题q:双曲线
=1表示焦点在y轴上的椭圆;命题q:双曲线 ![]() ﹣
﹣ ![]() =1的离心率e∈(1,2).若命题p、q有且只有一个为真,求m的取值范围.
=1的离心率e∈(1,2).若命题p、q有且只有一个为真,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A,B,C在圆x2+y2=1上运动,且AB⊥BC,若点P的坐标为 ![]() ,则
,则 ![]() 的取值范围为( )
的取值范围为( )
A.[8,10]
B.[9,11]
C.[8,11]
D.[9,12]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某餐馆一天中要购买A,B两种蔬菜每斤的价格分别为2元和3元,根据需要,A种蔬菜至少要买6斤,B种蔬菜至少要买4斤,而且一天中购买这两种蔬菜的总费用不能超过60元. 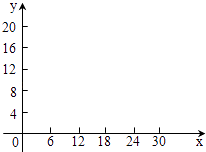
(1)写出一天中A种蔬菜购买的数量x和B种蔬菜购买的数量y之间的不等式组;
(2)在下面给定的坐标系中画出(1)中不等式组表示的平面区域(用阴影表示),并求出它的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com