
【题目】已知直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的余弦值为( )
所成角的余弦值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】分析:设M、N、P分别为AB,BB1和B1C1的中点,得出AB1、BC1夹角为MN和NP夹角或其补角;根据中位线定理,结合余弦定理求出AC、MQ,MP和∠MNP的余弦值即可.
详解:如图所示,设M、N、P分别为AB,BB1和B1C1的中点,
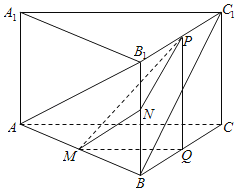
则AB1、BC1夹角为MN和NP夹角或其补角
(因异面直线所成角为(0,![]() ]),
]),
可知MN=![]() AB1=
AB1=![]() ,NP=
,NP=![]() BC1=
BC1=![]() ;
;
作BC中点Q,则△PQM为直角三角形;
∵PQ=1,MQ=![]() AC,
AC,
△ABC中,由余弦定理得
AC2=AB2+BC2﹣2ABBCcos∠ABC=4+1﹣2×2×1×(﹣![]() )=7,
)=7,
∴AC=![]() ,∴MQ=
,∴MQ=![]() ;
;
在△MQP中,MP=![]() =
=![]() ;
;
在△PMN中,由余弦定理得cos∠MNP=![]() =
= =﹣
=﹣![]() ;
;
又异面直线所成角的范围是(0,![]() ],
],
∴AB1与BC1所成角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调区间和极值.
的单调区间和极值.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)根据导数几何意义得![]() ,再与
,再与![]() 联立方程组解得
联立方程组解得![]() ,
, ![]() (2)先函数导数,再求导函数零点,列表分析导函数符号变化规律,进而确定单调区间和极值
(2)先函数导数,再求导函数零点,列表分析导函数符号变化规律,进而确定单调区间和极值
试题解析:(1)![]() ,切线为
,切线为![]() ,即斜率
,即斜率![]() ,纵坐标
,纵坐标![]()
即![]() ,
, ![]() ,解得
,解得![]() ,
, ![]()
解析式![]()
(2)![]()
![]()
![]() ,定义域为
,定义域为![]()
得到![]() 在
在![]() 单增,在
单增,在![]() 单减,在
单减,在![]() 单增
单增
极大值![]() ,极小值
,极小值![]() .
.
【题型】解答题
【结束】
20
【题目】如图:在四棱锥![]() 中,底面
中,底面![]() 为菱形,且
为菱形,且![]() ,
, ![]() 底面
底面![]() ,
,
![]() ,
, ![]() ,
, ![]() 是
是![]() 上点,且
上点,且![]() 平面
平面![]() .
.
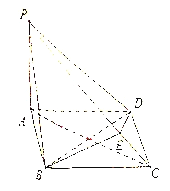
(1)求证: ![]() ;(2)求三棱锥
;(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在![]() 年的自主招生考试成绩中随机抽取
年的自主招生考试成绩中随机抽取![]() 名学生的笔试成绩,按成绩分组:第
名学生的笔试成绩,按成绩分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() 得到的频率分布直方图如图所示.
得到的频率分布直方图如图所示.

(1)分别求第![]() ,
, ![]() ,
, ![]() 组的频率;
组的频率;
(2)若该校决定在笔试成绩高的第![]() ,
, ![]() ,
, ![]() 组中用分层抽样抽取
组中用分层抽样抽取![]() 名学生进入第二轮面试,求第
名学生进入第二轮面试,求第![]() ,
, ![]() ,
, ![]() 组每组各抽取多少名学生进入第二轮面试?
组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受甲考官的面试,求第
名学生接受甲考官的面试,求第![]() 组至少有一名学生被甲考官面试的概率.
组至少有一名学生被甲考官面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() 为平面上一动点,
为平面上一动点,![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)不过原点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与直线
与直线![]() 交点的纵坐标为1,求
交点的纵坐标为1,求![]() 面积的最大值及此时直线
面积的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(Ⅰ)求{an}和{bn}的通项公式;
(Ⅱ)求数列{a2nbn}的前n项和(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图所示的程序框图,若输入的k=10,则该算法的功能是( ) 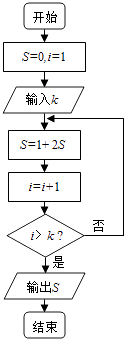
A.计算数列{2n﹣1}的前10项和
B.计算数列{2n﹣1}的前9项和
C.计算数列{2n﹣1}的前10项和
D.计算数列{2n﹣1}的前9项和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x(单位:小时)与当天投篮命中率y之间的关系:
时间x | 1 | 2 | 3 | 4 | 5 |
命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
小李这5天的平均投篮命中率为 ;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:


(1)设两种养殖方法的箱产量相互独立,记A表示事件“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率.
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
K2=![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,椭圆C和抛物线y2=x交于M,N两点,且直线MN恰好通过椭圆C的右焦点.
,椭圆C和抛物线y2=x交于M,N两点,且直线MN恰好通过椭圆C的右焦点.
(1)求椭圆C的标准方程;
(2)经过椭圆C右焦点的直线l和椭圆C交于A,B两点,点P在椭圆上,且 ![]() =2
=2 ![]() ,其中O为坐标原点,求直线l的斜率.
,其中O为坐标原点,求直线l的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com