
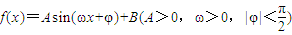 的图象上一个最高点的坐标为
的图象上一个最高点的坐标为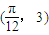 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为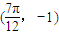 .
.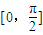 上的最大、最小值.
上的最大、最小值. 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 12 |
| 7π |
| 12 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| 3 |
| m |
| n |
| π |
| 12 |
| 7π |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 12 |
| 7π |
| 12 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 12 |
| 7π |
| 12 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2010年福建省泉州市南安市鹏峰中学高考数学模拟试卷1(文科)(解析版) 题型:解答题
 =(1,cos⊙x),
=(1,cos⊙x), =(sin⊙x,
=(sin⊙x,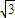 )(⊙>o),函数f(x)=
)(⊙>o),函数f(x)= 的图象上一个最高点的坐标为(
的图象上一个最高点的坐标为( ,2),与之相邻的一个最低点的坐标(
,2),与之相邻的一个最低点的坐标( ,-2).
,-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com