
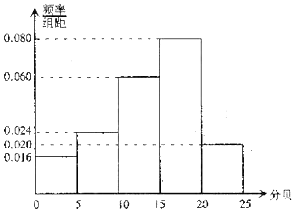
 人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db(分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀,某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:
人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db(分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀,某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:分析 (Ⅰ)根据题意得X的可能值为0,1,2,3,4,
求出对应的概率,写出X的分布列,计算数学期望值;
(Ⅱ)序号a1,a2,a3,a4的排列总数为${A}_{4}^{4}$,
计算Y≤2对应的种数为Y=0或Y=2时共4种,求出对应的概率值.
解答 解:(Ⅰ)X的可能值为0,1,2,3,4,
则P(X=0)=$\frac{{C}_{6}^{4}}{{C}_{10}^{4}}$=$\frac{15}{210}$,P(X=1)=$\frac{{C}_{4}^{1}{C}_{6}^{3}}{{C}_{10}^{4}}$=$\frac{80}{210}$,
P(X=2)=$\frac{{C}_{4}^{2}{C}_{6}^{2}}{{C}_{10}^{4}}$=$\frac{90}{210}$,P(X=3)=$\frac{{C}_{4}^{3}{•C}_{6}^{1}}{{C}_{10}^{4}}$=$\frac{24}{210}$,
P(X=4)=$\frac{{C}_{4}^{4}}{{C}_{10}^{4}}$=$\frac{1}{210}$;
∴X的分布列为
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{15}{210}$ | $\frac{80}{210}$ | $\frac{90}{210}$ | $\frac{24}{210}$ | $\frac{1}{210}$ |
点评 本题主要考查了离散型随机变量的分布列与数学期望的应用问题,是综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22017-1 | B. | 22017-2 | C. | $\frac{1}{3}({{4^{2017}}-1})$ | D. | $\frac{2}{3}({{4^{2017}}-1})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
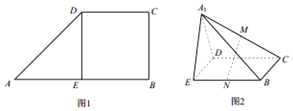 如图1.在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2CD,DE⊥AB,沿DE将△AEDD折起到△A1ED的位置,连结A1B,A1C,M,N分别为A1C,BE的中点.如图2.
如图1.在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2CD,DE⊥AB,沿DE将△AEDD折起到△A1ED的位置,连结A1B,A1C,M,N分别为A1C,BE的中点.如图2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com