Question

【题目】已知函数y=f（x）的图象与g（x）=logax（a＞0，且a≠1）的图象关于x轴对称，且g（x）的图象过（4，2）点．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若f（x﹣1）＞f（5﹣x），求x的取值范围．

Answer 1

【答案】解：（Ⅰ）∵g（x）=logax（a＞0，且a≠1）的图象过点（4，2），
∴loga4=2，a=2，则g（x）=log2x．
∵函数y=f（x）的图象与g（X）的图象关于x轴对称，
∴ ．
（Ⅱ）∵f（x﹣1）＞f（5﹣x），
∴ ，
即 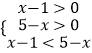，解得1＜x＜3，
所以x的取值范围为（1，3）
【解析】（Ⅰ）把点（4，2）代入g（x）的解析式求出a，再根据条件求出f（x）的解析式；（Ⅱ）根据（Ⅰ）和对数函数的单调性、真数大于零列出不等式组，求出解集即可．
【考点精析】通过灵活运用对数函数的单调性与特殊点，掌握过定点（1，0），即x=1时，y=0;a>1时在（0，+∞）上是增函数;0>a>1时在（0，+∞）上是减函数即可以解答此题．