
【题目】随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加.下表是某购物网站2018年1月~8月促销费用(万元)和产品销量(万件)的具体数据.
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
促销费用 | 2 | 3 | 6 | 10 | 13 | 21 | 15 | 18 |
产品销量 | 1 | 1 | 2 | 3 | 3.5 | 5 | 4 | 4.5 |
(1)根据数据可知![]() 与
与![]() 具有线性相关关系,请建立
具有线性相关关系,请建立![]() 与
与![]() 的回归方程
的回归方程![]() (系数精确到0.01);
(系数精确到0.01);
(2)已知6月份该购物网站为庆祝成立1周年,特制定奖励制度:以![]() (单位:件)表示日销量,
(单位:件)表示日销量,![]() ,则每位员工每日奖励100元;
,则每位员工每日奖励100元;![]() ,则每位员工每日奖励150元,
,则每位员工每日奖励150元,![]() ,则每位员工每日奖励200元.现已知该网站6月份日销量
,则每位员工每日奖励200元.现已知该网站6月份日销量![]() 服从正态分布
服从正态分布![]() ,请你计算某位员工当月奖励金额总数大约多少元(当月奖励金额总数精确到百分位).
,请你计算某位员工当月奖励金额总数大约多少元(当月奖励金额总数精确到百分位).
参考数据:![]() ,
,![]() ,其中
,其中![]() ,
,![]() 分别为第
分别为第![]() 个月的促销费用和产品销量,
个月的促销费用和产品销量,![]() .
.
参考公式:①对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为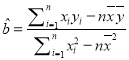 ,
,![]() ;②若随机变量
;②若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】设正整数数列![]() 满足
满足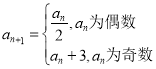 .
.
(1)若![]() ,请写出所有可能的
,请写出所有可能的![]() 的取值;
的取值;
(2)求证:![]() 中一定有一项的值为1或3;
中一定有一项的值为1或3;
(3)若正整数m满足当![]() 时,
时,![]() 中存在一项值为1,则称m为“归一数”,是否存在正整数m,使得m与
中存在一项值为1,则称m为“归一数”,是否存在正整数m,使得m与![]() 都不是“归一数”?若存在,请求出m的最小值;若不存在,请说明理由.
都不是“归一数”?若存在,请求出m的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
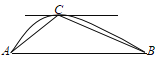
【题目】如图所示,设![]() ,
,![]() 是某抛物线上相异两点,将抛物线在
是某抛物线上相异两点,将抛物线在![]() ,
,![]() 之间的弧线与线段
之间的弧线与线段![]() 围成的区域记为
围成的区域记为![]() ;弧线
;弧线![]() 上取一点
上取一点![]() ,使抛物线在
,使抛物线在![]() 点处的切线与线段
点处的切线与线段![]() 平行,则三角形
平行,则三角形![]() 内部记为区域
内部记为区域![]() .古希腊伟大的哲学家、数学家、物理学家阿基米德在公元前3世纪,巧妙地证明了
.古希腊伟大的哲学家、数学家、物理学家阿基米德在公元前3世纪,巧妙地证明了![]() 与
与![]() 两区域的面积之比为常数,并求出了该常数的值.以抛物线
两区域的面积之比为常数,并求出了该常数的值.以抛物线![]() 上两点
上两点![]() ,
,![]() 之间的弧线为特例,探求该常数的值,并计算:向区域
之间的弧线为特例,探求该常数的值,并计算:向区域![]() 内任意投掷一点,则该点落在
内任意投掷一点,则该点落在![]() 内的概率是( )
内的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,直线
轴不重合,直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)证明![]() 为定值,并写出点
为定值,并写出点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 且与直线
且与直线![]() 垂直的直线与圆
垂直的直线与圆![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲,AD,BC是等腰梯形CDEF的两条高,![]() ,点M是线段AE的中点,将该等腰梯形沿着两条高AD,BC折叠成如图乙所示的四棱锥P-ABCD(E,F重合,记为点P).
,点M是线段AE的中点,将该等腰梯形沿着两条高AD,BC折叠成如图乙所示的四棱锥P-ABCD(E,F重合,记为点P).
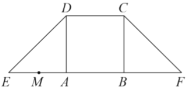
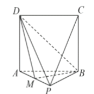
甲 乙
(1)求证:![]() ;
;
(2)求点M到平面BDP距离h.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有极值,且导函数
有极值,且导函数![]() 的极值点是
的极值点是![]() 的零点,给出命题:①
的零点,给出命题:①![]() ;②若
;②若![]() ,则存在
,则存在![]() ,使得
,使得![]() ;③若
;③若![]() 有两个极值点
有两个极值点![]() ,
,![]() ,则
,则![]() ;④若
;④若![]() ,且
,且![]() 是曲线
是曲线![]() ,
,![]() 的一条切线,则
的一条切线,则![]() 的取值范围是
的取值范围是![]() ;则以上命题正确序号是______.
;则以上命题正确序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个三位数的个位数字大于十位数字,十位数字大于百位数字,我们就称这个三位数为“递增三位数”.现从所有的递增三位数中随机抽取一个,则其三个数字依次成等差数列的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级 | 参赛人数 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 45 | 83 | 86 | 85 | 82 |
乙 | 45 | 83 | 84 | 85 | 133 |
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数少于甲班优秀的人数(竞赛得分![]() 分为优秀);
分为优秀);
③甲、乙两班成绩为85分的学生人数比成绩为其他值的学生人数多;
④乙班成绩波动比甲班小.
其中正确结论有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com