
【题目】已知函数![]() ,
,![]() .
.
(I)设![]() ,求
,求![]() 的单调区间;
的单调区间;
(II)若![]() 在
在![]() 处取得极大值,求实数
处取得极大值,求实数![]() 的取值范围.
的取值范围.
【答案】(I)单调增区间是![]() ,单调减区间是
,单调减区间是![]() .(II)
.(II)![]()
【解析】
试题分析:(I)![]() ,先求
,先求![]() 导函数
导函数![]() ,求导函数零点
,求导函数零点![]() ,列表分析导函数符号变化规律,确定单调区间(II)由题意得
,列表分析导函数符号变化规律,确定单调区间(II)由题意得![]() ,且
,且![]() 最大值;
最大值;![]() 最大值;而
最大值;而![]() 所以
所以![]() ,也可分类讨论单调性变化规律
,也可分类讨论单调性变化规律
试题解析:解:(I)∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() .
.
当![]() 时,在
时,在![]() 上
上![]() ,
,![]() 单调递增;
单调递增;
在![]() 上
上![]() ,
,![]() 单调递减.
单调递减.
∴![]() 的单调增区间是
的单调增区间是![]() ,单调减区间是
,单调减区间是![]() .
.
(II)∵![]() 在
在![]() 处取得极大值,∴
处取得极大值,∴![]() .
.
①当![]() ,即
,即![]() 时,由(I)知
时,由(I)知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时,![]() ,
,![]() 单调递减,不合题意;
单调递减,不合题意;
②当![]() ,即
,即![]() 时,由(I)知,
时,由(I)知,![]() 在
在![]() 上单调递增,
上单调递增,
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 处取得极小值,不合题意;
处取得极小值,不合题意;
③当![]() ,即
,即![]() 时,由(I)知,
时,由(I)知,![]() 在
在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时,![]() 取得极大值,满足条件.
取得极大值,满足条件.
综上,实数![]() 的取值范围是
的取值范围是![]()


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() N*
N*
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知![]() (
(![]() N*),记
N*),记![]()
![]() (
(![]() 且
且![]() ),是否存在这样的常数
),是否存在这样的常数![]() ,使得数列
,使得数列![]() 是常数列,若存在,求出
是常数列,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若数列![]() ,对于任意的正整数
,对于任意的正整数![]() ,均有
,均有
 成立,求证:数列
成立,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD 中,AB∥CD ,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别为CD和PC的中点.求证:
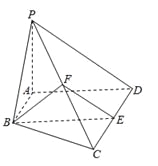
(1)BE∥平面PAD;
(2)平面BEF⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() 上任意一点M满足
上任意一点M满足![]() , 其中F
, 其中F![]() (-
(-![]() F
F![]() (
(![]() 抛物线
抛物线![]() 的焦点是直线y=x-1与x轴的交点, 顶点为原点O.
的焦点是直线y=x-1与x轴的交点, 顶点为原点O.
(I)求![]() ,
, ![]() 的标准方程;
的标准方程;
(II)请问是否存在直线l满足条件:① 过![]() 的焦点
的焦点![]() ;② 与
;② 与![]() 交于不同两点
交于不同两点![]() ,
, ![]() 且满足
且满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市组织500名志愿者参加敬老活动,为方便安排任务将所有志愿者按年龄(单位:岁)分组,得到的频率分布表如下.现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人担任联系人.
年龄(岁) | 频率 | |
第1组 | [25,30) | 0.1 |
第2组 | [30,35) | 0.1 |
第3组 | [35,40) | 0.4 |
第4组 | [40,45) | 0.3 |
第5组 | [45,50) | 0.1 |
(I)应分别在第1,2,3组中抽取志愿者多少人?
(II)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图:
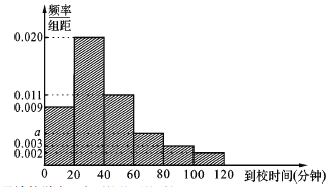
(1)求![]() 的值及该校学生从家到校的平均时间;
的值及该校学生从家到校的平均时间;
(2)若该校因学生寝室不足,只能容纳全校![]() 的学生住校,出于安全角度考虑,从家到校时间较长的学生才住校,请问从家到校时间多少分钟以上开始住校.
的学生住校,出于安全角度考虑,从家到校时间较长的学生才住校,请问从家到校时间多少分钟以上开始住校.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60), ...,[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 从成绩在[40,50)和[90,100]的学生中任选两人,求他们在同一分数段的概率.
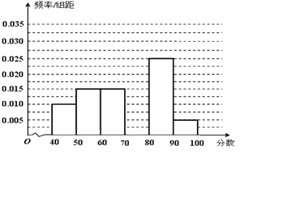
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com