
【题目】设函数![]() .
.
(1)若![]() 是偶函数,求k的值;
是偶函数,求k的值;
(2)设不等式![]() 的解集为A,若
的解集为A,若![]() ,求实数m的取值范围;
,求实数m的取值范围;
(3)设函数![]() ,若g(x)在
,若g(x)在![]() 有零点,求实数
有零点,求实数![]() 的取值范围.
的取值范围.
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】按照《国务院关于印发“十三五”节能减排综合工作方案的通知》(国发〔2016〕74号)的要求,到2020年,全国二氧化硫排放总量要控制在1580万吨以内,要比2015年下降15%.假设“十三五”期间每一年二氧化硫排放总量下降的百分比都相等,2015年后第![]() 年的二氧化硫律放总量最大值为
年的二氧化硫律放总量最大值为![]() 万吨.
万吨.
(1)求![]() 的解析式;
的解析式;
(2)求2019年全国二氧化赖持放总量要控制在多少万晚以内(精确到1万吨).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理财公司有两种理财产品A和B,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品A
投资结果 | 获利40% | 不赔不赚 | 亏损20% |
概率 |
|
|
|
产品B
投资结果 | 获利20% | 不赔不赚 | 亏损10% |
概率 | p |
| q |
注:p>0,q>0
(1)已知甲、乙两人分别选择了产品A和产品B投资,如果一年后他们中至少有一人获利的概率大于![]() ,求实数p的取值范围;
,求实数p的取值范围;
(2)若丙要将家中闲置的10万元人民币进行投资,以一年后投资收益的期望值为决策依据,则选用哪种产品投资较理想?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为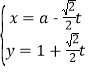 (
(![]() 为参数,
为参数,![]() ),以坐标原点为极点,以
),以坐标原点为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点(
两点(![]() 在
在![]() 之间),且
之间),且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com