
 对某班40名高中学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二维条形图如图所示.
对某班40名高中学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二维条形图如图所示.| 喜欢数学课程 | 不喜欢数学课程 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 | 40 |
| P(K2≥k0) | 0.5 | 0.4 | 0.25 | 0.15 | 0.1 | 0.01 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 6.635 |
分析 (1)根据条形图所给数据,得2×2列联表;根据列联表所给的数据,代入求观测值的公式,求出观测值,即可得出结论.
(2)确定基本事件的个数,利用公式求出女生A被选中的概率.
解答 解:(1)根据条形图所给数据,得2×2列联表为
| 喜欢数学课程 | 不喜欢数学课程 | 总计 | |
| 男 | 15 | 10 | 25 |
| 女 | 5 | 10 | 15 |
| 总计 | 20 | 20 | 40 |
点评 本题考查独立性检验的应用,考查概率的计算,本题解题的关键是正确利用观测值公式求出观测值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届安徽淮北十二中高三上月考二数学(文)试卷(解析版) 题型:解答题
已知函数 .
.
(1)当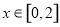 时,函数
时,函数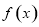 恒有意义,求实数
恒有意义,求实数 的取值范围;
的取值范围;
(2)是否存在这样的实数 ,使得函数
,使得函数 在区间
在区间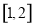 上为减函数,并且最大值为1?如果存在?试求出
上为减函数,并且最大值为1?如果存在?试求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平均数 | B. | 方差 | C. | 回归分析 | D. | 独立性检验 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com