
【题目】在下列各函数中,最小值等于2的函数是( )
A.y=x+ ![]()
B.y=cosx+ ![]() (0<x<
(0<x< ![]() )
)
C.y= ![]()
D.y= ![]()
 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】对于实数x,记[x]表示不超过x的最大整数,如[3.14]=3,[﹣0.25]=﹣1.若存在实数t,使得[t]=1,[t2]=2,[t3]=3…[tt]=n同时成立,则正整数n的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB、PB的中点 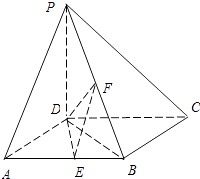
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论;
(3)求DB与平面DEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)
一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片.
(Ⅰ)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于7的概率;
(Ⅱ)若第一次随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字2的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com