
【题目】设![]() 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且![]() 满足:当
满足:当![]() 成立时,总可推出
成立时,总可推出
![]() 成立,那么下列命题总成立的是( )
成立,那么下列命题总成立的是( )
A. 若![]() 成立,则
成立,则![]() 成立;
成立;
B. 若![]() 成立,则
成立,则![]() 成立;
成立;
C. 若![]() 成立,则当
成立,则当![]() 时,均有
时,均有![]() 成立;
成立;
D. 若![]() 成立,则当
成立,则当![]() 时,均有
时,均有![]() 成立.
成立.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的方程为
的方程为![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
(1)求过点![]() 且与圆
且与圆![]() 相切的直线方程;
相切的直线方程;
(2)过点![]() 任作一条直线
任作一条直线![]() 与圆
与圆![]() 交于不同两点
交于不同两点![]() ,
,![]() ,且圆
,且圆![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,求证:直线
,求证:直线![]() 与
与![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1.M是棱SB的中点. (Ⅰ)求证:AM∥面SCD;
(Ⅱ)求面SCD与面SAB所成二面角的余弦值;
(Ⅲ)设点N是直线CD上的动点,MN与面SAB所成的角为θ,求sinθ的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (b∈R).若存在x∈[
(b∈R).若存在x∈[ ![]() ,2],使得f(x)+xf′(x)>0,则实数 b的取值范围是( )
,2],使得f(x)+xf′(x)>0,则实数 b的取值范围是( )
A.(﹣∞, ![]() )
)
B.(﹣∞, ![]() )
)
C.(﹣∞,3)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把![]() …这样的数称为“三角形数”,而把
…这样的数称为“三角形数”,而把![]() …
…
这样的数称为“正方形数”.如图,可以发现任何一个大于![]() 的“正方形数”都可以看作两个相邻
的“正方形数”都可以看作两个相邻
“三角形数”之和,下列四个等式:①![]() ;②
;②![]() ;③
;③![]() ;
;
④![]() 中符合这一规律的等式是_____________.(填写所有正确结论的编号)
中符合这一规律的等式是_____________.(填写所有正确结论的编号)

……
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是定义域为R的奇函数,当x∈[0,+∞)时,f(x)=x2-2x.
(1)写出函数y=f(x)的解析式
(2)若方程f(x)=a恰有3个不同的解,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
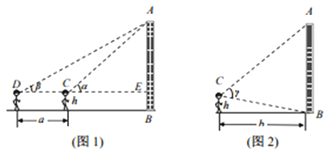
【题目】某校高一数学研究小组测量学校的一座教学楼AB的高度![]() 已知测角仪器距离地面的高度为h米,现有两种测量方法:
已知测角仪器距离地面的高度为h米,现有两种测量方法:
方法![]() 如图
如图![]() 用测角仪器,对准教学楼的顶部A,计算并记录仰角
用测角仪器,对准教学楼的顶部A,计算并记录仰角![]() ;
;![]() 后退a米,重复
后退a米,重复![]() 中的操作,计算并记录仰角
中的操作,计算并记录仰角![]() .
.
方法![]() 如图
如图![]() 用测角仪器,对准教学楼的顶部A底部B,测出教学楼的视角
用测角仪器,对准教学楼的顶部A底部B,测出教学楼的视角![]() ,测试点与教学楼的水平距离b米.
,测试点与教学楼的水平距离b米.
请你回答下列问题:
![]() 用数据
用数据![]() ,
,![]() ,a,h表示出教学楼AB的高度;
,a,h表示出教学楼AB的高度;
![]() 按照方法II,用数据
按照方法II,用数据![]() ,b,h表示出教学楼AB的高度.
,b,h表示出教学楼AB的高度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为![]() 的圆,满足下列条件:圆心
的圆,满足下列条件:圆心![]() 位于
位于![]() 轴正半轴上,与直线
轴正半轴上,与直线![]() 相切,且被
相切,且被![]() 轴截得的弦长为
轴截得的弦长为![]() ,圆
,圆![]() 的面积小于13.
的面积小于13.
(1)求圆![]() 的标准方程;
的标准方程;
(2)若点![]() ,点
,点![]() 是圆
是圆![]() 上一点,点
上一点,点![]() 是
是![]() 的重心,求点
的重心,求点![]() 的轨迹方程;
的轨迹方程;
(3)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,以
,以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() .是否存在这样的直线
.是否存在这样的直线![]() ,使得直线
,使得直线![]() 与
与![]() 恰好平行?如果存在,求出
恰好平行?如果存在,求出![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com