练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数

    （I）求证函数有两个零点；

    （II）设x1，x2是函数的两个零点，求| x1－x2|的范围；

    （III）求证函数的零点x1，x2至少有一个在区间（0，2）内.

    （I）证明：

     

    又

    故函数有两个零点

    （II）若的两个零点，

    则的两根                                               

     

    故

    （III）

    由（I）知

     

       （i）当

    又

    在区间（0，1）内至少有一个零点

    （ii）当

    在区间（1，2）内有一零点，

    综合（i）（ii），可知函数在区间（0，2）内至少有一个零点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2012•潍坊二模）已知函数f（x）=ax+x2，g（x）=xlna．a＞1．
    （I）求证函数F（x）=f（x）-g（x）在（0，+∞）上单调递增；
    （II）若函数y=|F(x)-b+
    1b
    |-3    有四个零点，求b的取值范围；
    （III）若对于任意的x1，x2∈[-1，1]时，都有|F(x2)-F(x1)|≤e2-2恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：北京市海淀区2007－2008学年度高三年级第一学期期中练习、数学试题(理科) 题型：044

    设函数f(x)的定义域为R，若|f(x)|≤|x|对一切实数x均成立，则称函数f(x)为Ω函数．

    (I)试判断函数f1(x)＝xsinx、和中哪些是Ω函数，并说明理由；

    (II)若函数y＝f(x)是定义在R上的奇函数，且满足对一切实数x1、x2，均有|f(x1)－f(x2)|≤|x1－x2|，求证：函数f(x)一定是Ω函数；

    (III)求证：若a＞1，则函数f(x)＝ln(x2＋a)－lna是Ω函数．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河北省高三12月月考试题理科数学 题型：解答题

    （本小题满分12分）

            设M是由满足下列条件的函数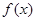构成的集合：“①方程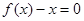有实数根；②函数”

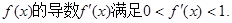       （I）判断函数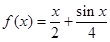是否是集合M中的元素，并说明理由；

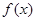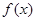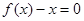       （II）集合M中的元素具有下面的性质：若 的定义域为D，则对于任意成立。试用这一性质证明：方程只有一个实数根；

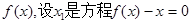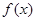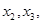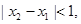    （III）对于M中的函数 的实数根，求证：对于定义域中任意的当且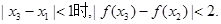

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年贵州省7校高三联考理数试题 题型：填空题

    （本小题满分12分）

    已知函数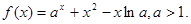

     （I）求证：函数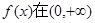上单调递增；

     （II）若方程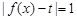有三个不同的实根，求t的值；

    （III）对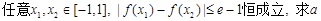的取值范围。

     

    查看答案和解析>>

    同步练习册答案