

分析 (1)在三棱柱ABC-A1B1C1中,要证:AB⊥平面BCC1B1;只需证明AB垂直平面内的两条相交直线,BC和BB1即可.
(2)求平面APQ将三棱柱ABC-A1B1C1分成上、下两部分几何体的体积之比,先求下部四棱锥的体积,再求棱柱的体积,然后求出两部分体积比.
(3)以B为原点,BA为x轴,BC为y轴,BB1为z轴,建立空间直角坐标系,由向量法能求出直线AQ与平面A1C1P不平行.
解答 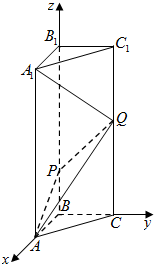 证明:(1)∵AB=3,BC=4,
证明:(1)∵AB=3,BC=4,
∴AC=12-3-4=5,
从而有AC2=AB2+BC2,∴AB⊥BC,
又∵AB⊥BB1,BC∩BB1=B,
∴AB⊥平面BCC1B1.
解:(2)∵BP=AB=3,CQ=AC=7,
∴SBCQP=$\frac{(BP+CQ)•BC}{2}$=$\frac{(3+7)×4}{2}$=20,
∴VA-BCQP=$\frac{1}{3}{S}_{BCQP}•AB=\frac{1}{3}×20×3$=20.
又∵${V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$=SABC•AA1=$\frac{1}{2}×3×4×12=72$,
∴平面APQ将三棱柱ABC-A1B1C1分成上、下两部分几何体的体积之比为:$\frac{{V}_{上}}{{V}_{下}}$=$\frac{72-20}{20}=\frac{13}{5}$.
(3)直线AQ与平面A1C1P不平行.
理由如下:
以B为原点,BA为x轴,BC为y轴,BB1为z轴,建立空间直角坐标系,
A(3,0,0),Q(0,4,7),A1(3,0,12),C1(0,5,12),P(0,0,3),
$\overrightarrow{AQ}$=(-3,4,7),$\overrightarrow{P{A}_{1}}$=(3,0,9),$\overrightarrow{P{C}_{1}}$=(0,5,9),
设平面A1C1P的法向量$\overrightarrow{n}=(x,y,z)$,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{P{A}_{1}}=3x+9z=0}\\{\overrightarrow{n}•\overrightarrow{P{C}_{1}}=5y+9z=0}\end{array}\right.$,取x=3,得$\overrightarrow{n}$=(3,$\frac{9}{5}$,-1),
∵$\overrightarrow{AQ}•\overrightarrow{n}$=-9+$\frac{36}{5}$-7=$\frac{46}{5}$≠0,
∴直线AQ与平面A1C1P不平行.
点评 本题考查直线与平面垂直,棱锥、棱柱的体积求法,考查线面是否平行的判断,考查空间想象能力,是中档题,解题时要注意向量法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 5 | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com