
【题目】某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样,回答问题统计结果如图表所示.

组别 | 分组 | 回答正确的人数 | 回答正确的人数占本组的概率 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) |
| 0.9 |
第3组 | [35,45) | 27 |
|
第4组 | [45,55) |
| 0.36 |
第5组 | [55,65) | 3 |
|
(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
【答案】(1)![]() ;(2)
;(2)![]() 人,
人,![]() 人,1人;(3)
人,1人;(3)![]() .
.
【解析】
试题(1)由统计表可求得第1组的人数,再由频率分布直方图可得到第1组人数点总体人数的频率(等于对应矩形方块的高度![]() 矩形方块的宽度),从而就可得到总体的人数n;进而就可求得其余各组的人数,再由统计表就可计算出a,b,x,y的值;(2)分层抽样方法就是各层按照相同的比例抽样:其抽取的比例为:
矩形方块的宽度),从而就可得到总体的人数n;进而就可求得其余各组的人数,再由统计表就可计算出a,b,x,y的值;(2)分层抽样方法就是各层按照相同的比例抽样:其抽取的比例为:![]() 结合(1)结果就可得到各组所抽取的人数;(3)将从(2)中抽取的6人按组别用不同的字母表示,然后用树图方式列出从中抽取2人的所有可能情况,数出全部情况总数,最后从中数出第2组至少有1人的情况的种数,从而就可求得所求的概率.
结合(1)结果就可得到各组所抽取的人数;(3)将从(2)中抽取的6人按组别用不同的字母表示,然后用树图方式列出从中抽取2人的所有可能情况,数出全部情况总数,最后从中数出第2组至少有1人的情况的种数,从而就可求得所求的概率.
试题解析:(1)第1组人数![]() , 所以
, 所以![]() ,
,
第2组人数![]() ,所以
,所以![]() ,
,
第3组人数![]() ,所以
,所以![]() ,
,
第4组人数![]() ,所以
,所以![]() ,
,
第5组人数![]() ,所以
,所以![]() . 5分
. 5分
(2)第2,3,4组回答正确的人的比为![]() ,所以第2,3,4组每组应各依次抽取
,所以第2,3,4组每组应各依次抽取![]() 人,
人,![]() 人,1人. 8分
人,1人. 8分
(3)记抽取的6人中,第2组的记为![]() ,第3组的记为
,第3组的记为![]() ,第4组的记为
,第4组的记为![]() , 则从6名幸运者中任取2名的所有可能的情况有15种,他们是:
, 则从6名幸运者中任取2名的所有可能的情况有15种,他们是:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() . 12分
. 12分
其中第2组至少有1人的情况有9种,他们是: ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
故所求概率为![]() . 14分
. 14分


科目:高中数学 来源: 题型:
【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了![]() 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(![]() (吨)为该商品进货量,
(吨)为该商品进货量, ![]() (天)为销售天数):
(天)为销售天数):
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅰ)根据上表数据在下列网格中绘制散点图;
(Ⅱ)根据上表提供的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)在该商品进货量![]() (吨)不超过6(吨)的前提下任取两个值,求该商品进货量
(吨)不超过6(吨)的前提下任取两个值,求该商品进货量![]() (吨)恰有一个值不超过3(吨)的概率.
(吨)恰有一个值不超过3(吨)的概率.
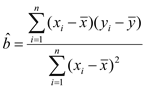 ,
,查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列命题:
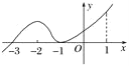
①-3是函数y=f(x)的极值点;
②-1是函数y=f(x)的最小值点;
③y=f(x)在区间(-3,1)上单调递增;
④y=f(x)在x=0处切线的斜率小于零.
以上正确命题的序号是( )
A. ①②B. ③④C. ①③D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一袋中有大小相同的4个红球和2个白球,给出下列结论:
①从中任取3球,恰有一个白球的概率是![]() ;
;
②从中有放回的取球6次,每次任取一球,则取到红球次数的方差为![]() ;
;
③现从中不放回的取球2次,每次任取1球,则在第一次取到红球的条件下,第二次再次取到红球的概率为![]() ;
;
④从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为![]() .
.
其中所有正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() ,若椭圆上一点与其中心及长轴一个端点构成等腰直角三角形.
,若椭圆上一点与其中心及长轴一个端点构成等腰直角三角形.
(Ⅰ)求椭圆E的离心率;
(Ⅱ)如图,若直线l与椭圆相交于AB且AB是圆![]() 的一条直径,求椭圆E的标准方程.
的一条直径,求椭圆E的标准方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理: “幂势既同,则积不容异”.意思是:夹在两个乎行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现将曲线![]() 绕
绕![]() 轴旋转一周得到的几何体叫做椭球体,记为
轴旋转一周得到的几何体叫做椭球体,记为![]() ,几何体
,几何体![]() 的三视图如图所示.根据祖暅原理通过考察
的三视图如图所示.根据祖暅原理通过考察![]() 可以得到
可以得到![]() 的体积,则
的体积,则![]() 的体积为( )
的体积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com