
【题目】已知某公司生产某产品的年固定成本为100万元,每生产1千件需另投入27万元,设该公司一年内生产该产品![]() 千件
千件![]() 并全部销售完,每千件的销售收入为
并全部销售完,每千件的销售收入为![]() 万元,且
万元,且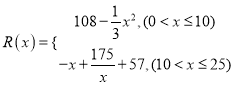 .
.
⑴ 写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
⑵ 当年产量为多少千件时,该公司在这一产品的生产中所获年利润最大?(注:年利润=年销售收入![]() 年总成本).
年总成本).
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣2)2+y2=9,直线l:x+y=0.
(1)求过圆C的圆心且与直线l垂直的直线n的方程;
(2)求与圆C相切,且与直线l平行的直线m的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax﹣1|﹣(a﹣1)x
(1)当a= ![]() 时,满足不等式f(x)>1的x的取值范围为;若函数f(x)的图象与x轴没有交点,则实数a的取值范围为 .
时,满足不等式f(x)>1的x的取值范围为;若函数f(x)的图象与x轴没有交点,则实数a的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|logax|(0<a<1)的定义域为[m,n](m<n),值域为[0,1],若n﹣m的最小值为 ![]() ,则实数a的值为( )
,则实数a的值为( )
A.![]()
B.![]() 或
或 ![]()
C.![]()
D.![]() 或
或 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E、F、G分别是棱SA、SB、SC的中点.求证: 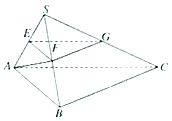
(1)平面EFG∥平面ABC;
(2)BC⊥平面SAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,下列条件:
①∠B+∠DAC=90°,
②∠B=∠DAC,
③![]() ,
,
④AB2=BD·BC.
其中一定能够判定△ABC是直角三角形的共有( )
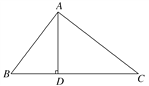
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R).
(1)证明:不论m取什么数,直线l与圆C恒交于两点;
(2)求直线l被圆C截得的线段的最短长度,并求此时m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点在原点,焦点在
的顶点在原点,焦点在![]() 轴上,且抛物线上有一点
轴上,且抛物线上有一点![]() 到焦点的距离为5.
到焦点的距离为5.
(1)求该抛物线![]() 的方程;
的方程;
(2)已知抛物线上一点![]() ,过点
,过点![]() 作抛物线的两条弦
作抛物线的两条弦![]() 和
和![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一位网民在网上光顾某网店,经过一番浏览后,对该店铺中的A,B,C三种商品有购买意向.已知该网民购买A种商品的概率为 ![]() ,购买B种商品的槪率为
,购买B种商品的槪率为 ![]() ,购买C种商品的概率为
,购买C种商品的概率为 ![]() .假设该网民是否购买这三种商品相互独立
.假设该网民是否购买这三种商品相互独立
(1)求该网民至少购买2种商品的概率;
(2)用随机变量η表示该网民购买商品的种数,求η的槪率分布和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com