
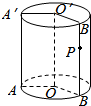
 如图,圆柱OO′的底面半径为2cm,高为4cm,且P为母线B′B的重点,∠AOB=120°,则一蚂蚁从A点沿圆柱表面爬到P点的最短路程为$\frac{2}{3}\sqrt{4{π}^{2}+9}$.
如图,圆柱OO′的底面半径为2cm,高为4cm,且P为母线B′B的重点,∠AOB=120°,则一蚂蚁从A点沿圆柱表面爬到P点的最短路程为$\frac{2}{3}\sqrt{4{π}^{2}+9}$. 分析 把AA',BB'展开到一个平面,得到一个矩形,矩形长即弧AB的长,再利用勾股定理,即可得出结论.
解答 解:把AA',BB'展开到一个平面,得到一个矩形,矩形长即弧AB的长,$\frac{2π}{3}$×2=$\frac{4π}{3}$,
∴一蚂蚁从A点沿圆柱表面爬到P点的最短路程为$\sqrt{(\frac{4π}{3})^{2}+{2}^{2}}$=$\sqrt{\frac{16{π}^{2}}{9}+4}$=$\frac{2}{3}\sqrt{4{π}^{2}+9}$.
故答案为:$\frac{2}{3}\sqrt{4{π}^{2}+9}$.
点评 本题考查蚂蚁从A点沿圆柱表面爬到P点的最短路程,考查展开图的运用,比较基础.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(a+b)(\frac{1}{a}+\frac{1}{b})≥4$ | B. | a3+b3≥2ab2 | C. | $\sqrt{|a-b|}≥\sqrt{a}-\sqrt{b}$ | D. | a2+b2+2≥2a+2b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知正方形ABCD和矩形ACEF所在平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点.用向量方法证明与解答:
如图,已知正方形ABCD和矩形ACEF所在平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点.用向量方法证明与解答:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com