【答案】
分析:(Ⅰ)利用两个向量的数量积公式化简函数f(x)的解析式为-2sin(2x-
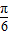
)+1,由此求得函数的最小正周期,令 2kπ-
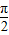
≤2x-
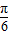
≤2kπ+

,k∈z,求得x的范围,即可求得
函数的单调递减区间.
(Ⅱ)由题意可得函数y=f(x)的图象和直线y=k 在区间
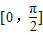
上有交点,由 0≤x≤
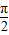
可得函数f(x)的值域,即为 k的取值范围.
解答:解:(Ⅰ)∵函数f(x)=
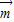
•
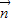
=2cos
2x-
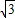
sin2x=cos2x-
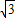
sin2x+1=2sin(
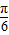
-2x)+1=-2sin(2x-
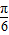
)+1,
∴函数的最小正周期为
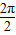
=π,令 2kπ-
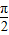
≤2x-
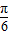
≤2kπ+
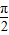
,k∈z,解得kπ-
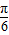
≤x≤kπ+
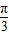
,k∈z,
故函数的减区间为[kπ-
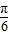
,kπ+
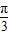
],k∈z.
(Ⅱ)若方程f(x)-k=0在区间
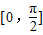
上有实数根,则函数y=f(x)的图象和直线y=k 在区间
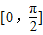
上有交点.
由 0≤x≤
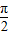
可得-
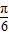
≤2x-
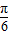
≤
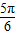
,∴-

≤sin(2x-

)≤1,∴-1≤-2sin(2x-
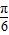
)+1≤2,
即函数f(x)的值域为[-1,2],
故-1≤k≤2,即k的取值范围为[-1,2].
点评:本题主要考查两个向量的数量积公式,两角和差的正弦公式,正弦函数的单调性、定义域和值域,函数的零点与方程的根的关系,体现了转化的数学思想,属于中档题.

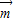 =
=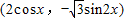 ,
,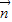 =(cosx,1),设函数f(x)=
=(cosx,1),设函数f(x)=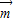 •
• ,x∈R.
,x∈R.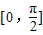 上有实数根,求k的取值范围.
上有实数根,求k的取值范围.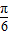 )+1,由此求得函数的最小正周期,令 2kπ-
)+1,由此求得函数的最小正周期,令 2kπ-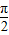 ≤2x-
≤2x-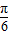 ≤2kπ+
≤2kπ+ ,k∈z,求得x的范围,即可求得
,k∈z,求得x的范围,即可求得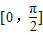 上有交点,由 0≤x≤
上有交点,由 0≤x≤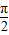 可得函数f(x)的值域,即为 k的取值范围.
可得函数f(x)的值域,即为 k的取值范围.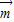 •
•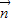 =2cos2x-
=2cos2x-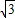 sin2x=cos2x-
sin2x=cos2x-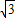 sin2x+1=2sin(
sin2x+1=2sin(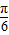 -2x)+1=-2sin(2x-
-2x)+1=-2sin(2x-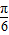 )+1,
)+1,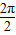 =π,令 2kπ-
=π,令 2kπ-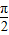 ≤2x-
≤2x-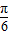 ≤2kπ+
≤2kπ+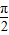 ,k∈z,解得kπ-
,k∈z,解得kπ-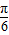 ≤x≤kπ+
≤x≤kπ+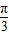 ,k∈z,
,k∈z,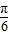 ,kπ+
,kπ+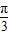 ],k∈z.
],k∈z.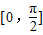 上有实数根,则函数y=f(x)的图象和直线y=k 在区间
上有实数根,则函数y=f(x)的图象和直线y=k 在区间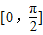 上有交点.
上有交点.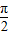 可得-
可得-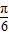 ≤2x-
≤2x-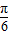 ≤
≤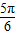 ,∴-
,∴- ≤sin(2x-
≤sin(2x- )≤1,∴-1≤-2sin(2x-
)≤1,∴-1≤-2sin(2x-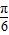 )+1≤2,
)+1≤2,

 阅读快车系列答案
阅读快车系列答案![]() ,
,![]() ,其中
,其中![]() ,且
,且![]() ,又函数
,又函数![]() 的图象任意两相邻对称轴间距为
的图象任意两相邻对称轴间距为![]() . w ww.ks 5u.co m
. w ww.ks 5u.co m![]() 的值;
的值;![]() 是第一象限角,且
是第一象限角,且![]() ,求
,求 的值.
的值.![]() ,
,![]() ,其中
,其中![]() ,且
,且![]() ,又函数
,又函数![]() 的图象任意两相邻对称轴间距为
的图象任意两相邻对称轴间距为![]() . w ww.ks 5u.co m
. w ww.ks 5u.co m![]() 的值;
的值;![]() 是第一象限角,且
是第一象限角,且![]() ,求
,求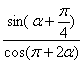 的值.
的值.