
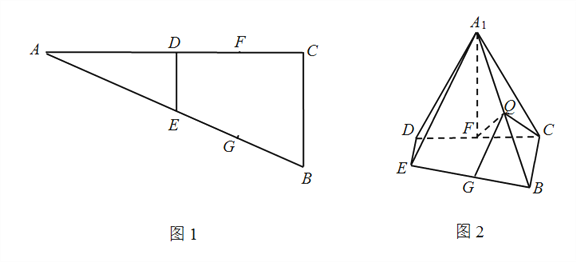
【题目】如图1,在![]() △
△![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为边
分别为边![]() 的中点,点
的中点,点![]() 分别为线段
分别为线段![]() 的中点.将△
的中点.将△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使
的位置,使![]() .点
.点![]() 为线段
为线段![]() 上的一点,如图2.
上的一点,如图2.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)线段![]() 上是否存在点
上是否存在点![]() 使得
使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长,若不存在,请说明理由;
的长,若不存在,请说明理由;
(Ⅲ)当![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(1)见解析(2)在线段![]() 上存在中点
上存在中点![]() ,使
,使![]() 平面
平面![]() .
.
且![]() (3)
(3)![]()
【解析】试题分析:(1)先根据等腰三角形性质得![]() .再由折叠中不变的垂直关系得
.再由折叠中不变的垂直关系得![]() ,根据线面垂直判定定理得
,根据线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]()
![]() .最后再根据线面垂直判定定理得
.最后再根据线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() .(2)利用空间向量研究线面平行关系,即通过平面法向量与直线方向向量垂直进行研究,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出平面法向量,利用向量数量积求直线方向向量与法向量夹角,最后根据平面法向量与直线方向向量数量积为零列式求解参数.(3)利用空间向量求线面角,仍是先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出平面法向量,利用向量数量积求直线方向向量与法向量夹角,最后根据线面角与向量夹角之间互余关系列式求线面角大小.
.(2)利用空间向量研究线面平行关系,即通过平面法向量与直线方向向量垂直进行研究,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出平面法向量,利用向量数量积求直线方向向量与法向量夹角,最后根据平面法向量与直线方向向量数量积为零列式求解参数.(3)利用空间向量求线面角,仍是先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出平面法向量,利用向量数量积求直线方向向量与法向量夹角,最后根据线面角与向量夹角之间互余关系列式求线面角大小.
试题解析:解:(Ⅰ)
因为![]() ,
,
所以△![]() 为等边三角形.
为等边三角形.
又因为点![]() 为线段
为线段![]() 的中点,
的中点,
所以![]() .
.
由题可知![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]()
![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() .
.
(Ⅱ)由(Ⅰ)知![]() 平面
平面![]() ,
, ![]() ,如图
,如图
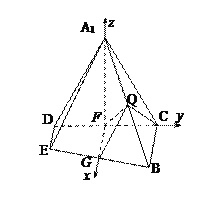
建立空间直角坐标系,则![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
![]() ,
,![]() ,
,
所以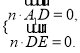 即
即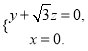
令![]() ,所以
,所以![]() ,所以
,所以![]()
假设在线段![]() 上存在点
上存在点![]() ,使img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/14/e30bb3b0/SYS201712291439006281273551_DA/SYS201712291439006281273551_DA.053.png" width="39" height="21" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />平面
,使img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/14/e30bb3b0/SYS201712291439006281273551_DA/SYS201712291439006281273551_DA.053.png" width="39" height="21" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />平面![]() .
.
设![]() ,
, ![]() .
.
又![]() ,所以
,所以![]() .
.
所以![]() .则
.则![]() .
.
所以![]() .
.
解得, ![]() .
.
则在线段![]() 上存在中点
上存在中点![]() ,使
,使![]() 平面
平面![]() .
.
且![]()
(Ⅲ)因为![]() ,又
,又![]() ,所以
,所以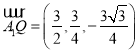 .
.
所以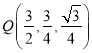 .又因为
.又因为![]() ,
,
所以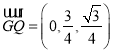 .
.
因为![]() 设直线
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则
直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.


科目:高中数学 来源: 题型:
【题目】己知集合M={﹣1,1,2,4}N={0,1,2}给出下列四个对应法则,其中能构成从M到N的函数是( )
A.y=x2
B.y=x+1
C.y=2x
D.y=log2|x|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个命题中:
①设有一个回归方程 ![]() =2﹣3x,变量x增加一个单位时,y平均增加3个单位;
=2﹣3x,变量x增加一个单位时,y平均增加3个单位;
②两个随机变量的线性相关性越强,则相关系数的绝对值越接近于1;
③在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0).若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8.
其中真命题的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准![]() (吨),用水量不超过
(吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() ,
, ![]() ,…,
,…, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
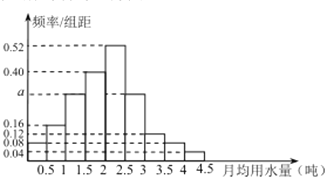
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使![]() 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由;
的值,并说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x)对任意x∈R都有f(x)=f(x+4),当x∈(﹣2,0)时,f(x)=2x , 则f(2016)﹣f(2015)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)证明f(x)为偶函数;
(2)若不等式k≤xf(x)+ ![]() 在x∈[1,3]上恒成立,求实数k的取值范围;
在x∈[1,3]上恒成立,求实数k的取值范围;
(3)当x∈[ ![]() ,
, ![]() ](m>0,n>0)时,函数g(x)=tf(x)+1,(t≥0)的值域为[2﹣3m,2﹣3n],求实数t的取值范围.
](m>0,n>0)时,函数g(x)=tf(x)+1,(t≥0)的值域为[2﹣3m,2﹣3n],求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角性”. 
该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )
A.2017×22015
B.2017×22014
C.2016×22015
D.2016×22014
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com