
分析 (1)分离常数得到f(x)=$2-\frac{1}{x+1}$,根据反比例函数的单调性便可看出f(x)的单调递增区间为(-∞,-1),(-1,+∞),根据单调性的定义证明:设任意的x1,x2≠-1,且x1<x2,然后作差,通分,说明x1,x2∈(-∞,-1),或x1,x2∈(-1,+∞)上时都有f(x1)<f(x2),这样即可得出f(x)的单调区间;
(2)根据f(x)的单调性便知f(x)在[3,5]上单调递增,从而可以求出f(x)的值域,从而可以得出f(x)在[3,5]上的最大、最小值.
解答 解:(1)$f(x)=\frac{2(x+1)-1}{x+1}=2-\frac{1}{x+1}$;
该函数的定义域为{x|x≠-1},设x1,x2∈{x|x≠-1},且x1<x2,则:
$f({x}_{1})-f({x}_{2})=\frac{1}{{x}_{2}+1}-\frac{1}{{x}_{1}+1}=\frac{{x}_{1}-{x}_{2}}{({x}_{1}+1)({x}_{2}+1)}$;
∵x1<x2;
∴x1-x2<0;
∴x1,x2∈(-∞,-1)时,x1+1<0,x2+1<0;x1,x2∈(-1,+∞)时,x1+1>0,x2+1>0;
∴(x1+1)(x2+1)>0;
∴f(x1)<f(x2);
∴f(x)在(-∞,-1),(-1,+∞)上单调递增,即f(x)的单调增区间为(-∞,-1),(-1,+∞);
(2)由上面知f(x)在[3,5]上单调递增;
∴f(3)≤f(x)≤f(5);
∴$\frac{7}{4}≤f(x)≤\frac{11}{6}$;
∴f(x)在[3,5]上的最大值为$\frac{11}{6}$,最小值为$\frac{7}{4}$.
点评 考查分离常数法的运用,反比例函数的单调性和单调区间,根据单调性的定义找函数单调区间的方法和过程,根据函数单调性求函数在闭区间上的最值.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 设a,b∈N*,记R(a\b)为a除以b所得的余数,执行如图所示的程序框图,若输入a=243,b=45,则输出的值等于( )
设a,b∈N*,记R(a\b)为a除以b所得的余数,执行如图所示的程序框图,若输入a=243,b=45,则输出的值等于( )| A. | 0 | B. | 1 | C. | 9 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 63 | B. | 31 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
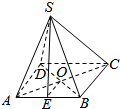 如图,S-ABCD是正四棱锥,已知底面边长AB=6cm,侧棱SA=3$\sqrt{5}$cm,求该正四棱锥的侧面SAB的斜高SE和底面AC所成角的大小.
如图,S-ABCD是正四棱锥,已知底面边长AB=6cm,侧棱SA=3$\sqrt{5}$cm,求该正四棱锥的侧面SAB的斜高SE和底面AC所成角的大小.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点,沿直线BD将△BCD翻折成△BC′D,使得平面BC′D⊥平面ABD.
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点,沿直线BD将△BCD翻折成△BC′D,使得平面BC′D⊥平面ABD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com