
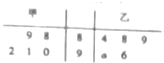
 某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0-9的某个整数
某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0-9的某个整数| 1 |
| 5 |
| 1 |
| 5 |
| S | 2 甲 |
| 1 |
| 5 |
| S | 2 乙 |
| 1 |
| 5 |
| S | 2 乙 |
| S | 2 甲 |
| C | 2 5 |
| C | 1 3 |
| C | 1 2 |
| C | 2 2 |
| 7 |
| 10 |


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
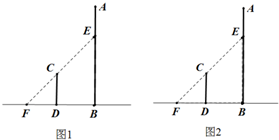 某公司为了公司周年庆典,现将公司门前广场进行装饰,广场上有一垂直于地面的墙面AB高为8+8
某公司为了公司周年庆典,现将公司门前广场进行装饰,广场上有一垂直于地面的墙面AB高为8+8| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、2
| ||
C、
| ||
D、2
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| n |
| ||
| n=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
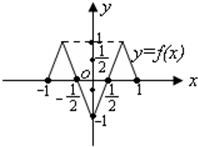 已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是
已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是查看答案和解析>>
科目:高中数学 来源: 题型:
| 访问量 | 500 | 600 | 700 |
| 频 数 | 50 | 30 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 3 |
| π |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com