
【题目】已知椭圆![]() 的左、右两个焦点分别为
的左、右两个焦点分别为![]() ,P是椭圆上位于第一象限内的点,
,P是椭圆上位于第一象限内的点,![]() 轴,垂足为Q,
轴,垂足为Q,![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .
.
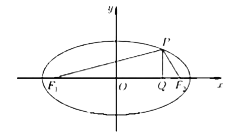
(1)求椭圆F的方程:
(2)若M是椭圆上的动点,求![]() 的最大值,并求出
的最大值,并求出![]() 取得最大值时M的坐标.
取得最大值时M的坐标.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】一位幼儿园老师给班上k(k≥3)个小朋友分糖果.她发现糖果盒中原有糖果数为a0,就先从别处抓2块糖加入盒中,然后把盒内糖果的![]() 分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的
分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的![]() 分给第二个小朋友;…,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的
分给第二个小朋友;…,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的![]() 分给第n(n=1,2,3,…k)个小朋友.如果设分给第n个小朋友后(未加入2块糖果前)盒内剩下的糖果数为an.
分给第n(n=1,2,3,…k)个小朋友.如果设分给第n个小朋友后(未加入2块糖果前)盒内剩下的糖果数为an.
(1)当k=3,a0=12时,分别求a1,a2,a3;
(2)请用an-1表示an;令bn=(n+1)an,求数列{bn}的通项公式;
(3)是否存在正整数k(k≥3)和非负整数a0,使得数列{an}(n≤k)成等差数列,如果存在,请求出所有的k和a0,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设动直线![]() :
:![]() 分别与曲线
分别与曲线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,求当
,求当![]() 为何值时,
为何值时,![]() 取最大值,并求
取最大值,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学在全校范围内举办了一场“中国诗词大会”的比赛,规定初赛测试成绩不小于160分的学生进入决赛阶段比赛.现有200名学生参加测试,并将所有测试成绩统计如下表:
分数段 | 频数 | 频率 |
| 6 | 0.03 |
|
| 0.38 |
| 100 | 0.5 |
|
|
|
| 6 | 0.03 |
合计 | 200 | 1 |
(1)计算![]() 的值;
的值;
(2)现利用分层抽样的方法从进入决赛的学生中选择6人,再从选出的6人中选2人做进一步的研究,求选择的2人中至少有1人的分数在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系xOy的坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程是![]() ,曲线C2的参数方程是
,曲线C2的参数方程是![]() (θ为参数).
(θ为参数).
(1)写出曲线C1,C2的普通方程;
(2)设曲线C1与y轴相交于A,B两点,点P为曲线C2上任一点,求|PA|2+|PB|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,点![]() 为半径为
为半径为![]() 千米的圆形海岛的最东端,点
千米的圆形海岛的最东端,点![]() 为最北端,在点
为最北端,在点![]() 的正东
的正东![]() 千米
千米![]() 处停泊着一艘缉私艇,某刻,发现在
处停泊着一艘缉私艇,某刻,发现在![]() 处有一小船正以速度
处有一小船正以速度![]() (千米/小时)向正北方向行驶,已知缉私艇的速度为
(千米/小时)向正北方向行驶,已知缉私艇的速度为![]() (千米/小时) .
(千米/小时) .
(1)为了在最短的时间内拦截小船检查,缉私艇应向什么方向行驶? (精确到![]() )
)
(2)海岛上有一快艇要为缉私艇送去给养,问选择海岛边缘的哪一点![]() 出发才能行程最短? (如图2建立坐标系, 用坐标表示点
出发才能行程最短? (如图2建立坐标系, 用坐标表示点![]() 的位置)
的位置)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心C在直线![]() 上.
上.
![]() 若圆C与y轴的负半轴相切,且该圆截x轴所得的弦长为
若圆C与y轴的负半轴相切,且该圆截x轴所得的弦长为![]() ,求圆C的标准方程;
,求圆C的标准方程;
![]() 已知点
已知点![]() ,圆C的半径为3,且圆心C在第一象限,若圆C上存在点M,使
,圆C的半径为3,且圆心C在第一象限,若圆C上存在点M,使![]() 为坐标原点
为坐标原点![]() ,求圆心C的纵坐标的取值范围.
,求圆心C的纵坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com