
【题目】已知m,n,s,t∈R+ , m+n=2, ![]() ,其中m、n是常数,当s+t取最小值
,其中m、n是常数,当s+t取最小值 ![]() 时,m、n对应的点(m,n)是双曲线
时,m、n对应的点(m,n)是双曲线 ![]() 一条弦的中点,则此弦所在的直线方程为 .
一条弦的中点,则此弦所在的直线方程为 .
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设m,n∈R,定义在区间[m,n]上的函数f(x)=log2(4﹣|x|)的值域是[0,2],若关于t的方程( ![]() )|t|+m+1=0(t∈R)有实数解,则m+n的取值范围是 .
)|t|+m+1=0(t∈R)有实数解,则m+n的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各小题中,p是q的充分不必要条件的是( ) ①p:m<﹣2或m>6,q:y=x2+mx+m+3有两个零点;
② ![]() ,q:y=f(x)是偶函数;
,q:y=f(x)是偶函数;
③p:cosα=cosβ,q:tanα=tanβ;
④p:A∩B=A,q:(UB)(UA)
A.①②
B.②③
C.③④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为抛物线y 2=﹣8x的焦点,O为原点,点P是抛物线准线上一动点,点A在抛物线上,且|AF|=4,则|PA|+|PO|的最小值为( )
A.6
B.![]()
C.![]()
D.4+2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且当x>0时,f(x)=lg ![]() ,若对任意实数t∈[
,若对任意实数t∈[ ![]() ,2],都有f(t+a)﹣f(t﹣1)≥0恒成立,则实数a的取值范围 .
,2],都有f(t+a)﹣f(t﹣1)≥0恒成立,则实数a的取值范围 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程是 ![]() (t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2+12ρcosθ+11=0. (Ⅰ)说明C是哪种曲线?并将C的方程化为直角坐标方程;
(t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2+12ρcosθ+11=0. (Ⅰ)说明C是哪种曲线?并将C的方程化为直角坐标方程;
(Ⅱ)直线l与C交于A,B两点,|AB|= ![]() ,求l的斜率.
,求l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为响应国家节能减排建设的号召,唤起人们从自己身边的小事做起,开展了以“再小的力量也是一种支持”为主题的宣传教育活动,其中有两则公益广告: ①80部手机,一年就会增加一吨二氧化氮的排放.
②人们在享受汽车带了的便捷舒适的同时,却不得不呼吸汽车排放的尾气.
活动组织者为了解是市民对这两则广告的宣传效果,随机对10﹣60岁的人群抽查了n人,并就两个问题对选取的市民进行提问,其抽样人数频率分布直方图如图所示,宣传效果调查结果如表所示.
宣传效果调查表
广告一 | 广告二 | |||
回答正 | 占本组 | 回答正 | 占本组 | |
[10,20) | 90 | 0.5 | 45 | a |
[20,30) | 225 | 0.75 | k | 0.8 |
[30,40) | b | 0.9 | 252 | 0.6 |
[40,50) | 160 | c | 120 | d |
[50,60] | 10 | e | f | g |
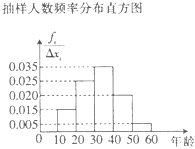
(1)分别写出n,a,b,c,d的值.
(2)若将表中的频率近似看作各年龄组正确回答广告内容的概率,规定正确回答广告一的内容得30元,广告二的内容得60元.组织者随机请一家庭的两成员(大人45岁,孩子17岁),指定大人回答广告一的内容,孩子回答广告二的内容,求该家庭获得奖金数ξ的分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com