
【题目】已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)若h(x)=g(x)﹣λf(x)+1在[﹣1,1]上是增函数,求实数λ的取值范围.
【答案】解:(Ⅰ)设g(x)任一点P(x0 , y0),则其关于原点对称点P'(﹣x0 , ﹣y0)在f(x)图象上, 则﹣y0=(﹣x0)2+(﹣x0),即y0=﹣x02+x0 ,
∴g(x)=﹣x2+x.
(Ⅱ)h(x)=﹣x2+x﹣λ(x2+x)+1=(﹣1﹣λ)x2+(1﹣λ)x+1;
即h(x)=(﹣1﹣λ)x2+(1﹣λ)x+1;
② 若λ=﹣1,h(x)=2x+1,满足在[﹣1,1]上是增函数;
②若λ≠﹣1,h(x)是二次函数,对称轴为x= ![]() ;
;
(ⅰ)当λ<﹣1时, ![]() ≤﹣1,解得﹣3≤λ<﹣1,
≤﹣1,解得﹣3≤λ<﹣1,
(ⅱ)当λ>﹣1时, ![]() ≥1,解得=1<λ≤﹣
≥1,解得=1<λ≤﹣ ![]() .
.
综上,﹣3≤λ≤﹣ ![]()
【解析】(Ⅰ)设g(x)任一点P(x0 , y0),则其关于原点对称点P'(﹣x0 , ﹣y0)在f(x)图象上,故有﹣y0=(﹣x0)2+(﹣x0),即y0=﹣x02+x0 , 从而得到函数g(x)的解析式.(Ⅱ)h(x)=(﹣1﹣λ)x2+(1﹣1λ)x+1,λ=﹣1时,h(x)=2x+1,在[﹣1,1]上是增函数;λ≠﹣1时,根据二次函数的单调性即可求得λ的范围,合并λ=﹣1即得λ的取值范围.
【考点精析】关于本题考查的函数单调性的判断方法,需要了解单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn+an=4,n∈N* .
(1)求数列{an}的通项公式;
(2)已知cn=2n+3(n∈N*),记dn=cn+logCan(C>0且C≠1),是否存在这样的常数C,使得数列{dn}是常数列,若存在,求出C的值;若不存在,请说明理由.
(3)若数列{bn},对于任意的正整数n,均有b1an+b2an﹣1+b3an﹣2+…+bna1=( ![]() )n﹣
)n﹣ ![]() 成立,求证:数列{bn}是等差数列.
成立,求证:数列{bn}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了测量山顶M的海拔高度,飞机沿水平方向在A,B两点进行测量,A,B,M在同一个铅垂面内(如图).能够测量的数据有俯角、飞机的高度和A,B两点间的距离.请你设计一个方案,包括: 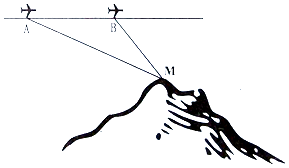
(1)指出需要测量的数据(用字母表示,并在图中标出);
(2)用文字和公式写出计算山顶M海拔高度的步骤.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱A1B1C1﹣ABC中, ![]() ,AB=AC=AA1=1,已知G和E分别为A1B1和CC1的中点,D与F分别为线段AC和AB上的动点(不包括端点),若GD⊥EF,则线段DF的长度的取值范围为( )
,AB=AC=AA1=1,已知G和E分别为A1B1和CC1的中点,D与F分别为线段AC和AB上的动点(不包括端点),若GD⊥EF,则线段DF的长度的取值范围为( )
A.[ ![]() ,1)
,1)
B.[ ![]() ,1]
,1]
C.( ![]() ,1)
,1)
D.[ ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项为1,Sn为数列{an}的前n项和,Sn+1=qSn+1,其中q>0,n∈N* .
(1)若2a2 , a3 , a2+2成等差数列,求数列{an}的通项公式;
(2)设数列{bn}满足bn= ![]() ,且b2=
,且b2= ![]() ,证明:b1+b2++bn>
,证明:b1+b2++bn> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别为双曲线C: ![]() ﹣
﹣ ![]() =1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1 , 则双曲线C的离心率e的取值范围是( )
=1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1 , 则双曲线C的离心率e的取值范围是( ) 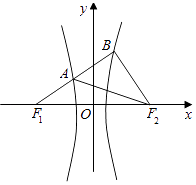
A.(3,+∞)
B.(1,2+ ![]() )
)
C.(3,2+ ![]() )
)
D.(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行环保知识竞赛,为了了解本次竞赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为正数,满分100分),进行统计,请根据频率分布表中所提供的数据,解答下列问题:
(Ⅰ)求a、b的值;
(Ⅱ)若从成绩较好的第3、4、5组中,按分层抽样的方法抽取6人参加社区志愿者活动,并从中选出2人做负责人,求2人中至少有1人是第四组的概率.
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60] | 5 | 0.05 |
第2组 | [60,70] | a | 0.35 |
第3组 | [70,80] | 30 | b |
第4组 | [80,90] | 20 | 0.20 |
第5组 | [90,100] | 10 | 0.10 |
合计 | 100 | 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为 ![]() .
.
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com