
【题目】已知定义域为R的奇函数y=f(x)的导函数为y=f′(x),当x≠0时, ![]() >0,若a=f(1),b=﹣2f(﹣2),c=(ln
>0,若a=f(1),b=﹣2f(﹣2),c=(ln ![]() )f(ln
)f(ln ![]() ),则a,b,c的大小关系正确的是( )
),则a,b,c的大小关系正确的是( )
A.a<c<b
B.b<c<a
C.a<b<c
D.c<a<b
【答案】D
【解析】解:设g(x)=xf(x), ![]() ; ∵x≠0时,
; ∵x≠0时, ![]() ;
;
∴x>0时,g′(x)>0;
∴g(x)在(0,+∞)上单调递增;
∵f(x)为奇函数;
∴b=﹣2f(﹣2)=2f(2), ![]() ;
;
又a=f(1)=1f(1);
∵ln2<1<2,g(x)在(0,+∞)上单调递增;
∴g(ln2)<g(1)<g(2);
即(ln2)f(ln2)<1f(1)<2f(2);
∴c<a<b.
故选:D.
根据a,b,c的表示形式构造函数g(x)=xf(x),根据条件可说明x>0时,g′(x)>0,这便得到g(x)在(0,+∞)上单调递增.而由f(x)为奇函数便可得到b=2f(2),c=(ln2)f(ln2),而容易判断ln2<1<2,从而得到g(ln2)<g(1)<g(2),这样便可得出a,b,c的大小关系.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求证:存在定点![]() ,使得函数
,使得函数![]() 图象上任意一点
图象上任意一点![]() 关于
关于![]() 点对称的点
点对称的点![]() 也在函数
也在函数![]() 的图象上,并求出点
的图象上,并求出点![]() 的坐标;
的坐标;
(2)定义![]() ,其中
,其中![]() 且
且![]() ,求
,求![]() ;
;
(3)对于(2)中的![]() ,求证:对于任意
,求证:对于任意![]() 都有
都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(x2+ax﹣a﹣1),给出下列命题:
①函数f(x)有最小值;
②当a=0时,函数f(x)的值域为R;
③若函数f(x)在区间(﹣∞,2]上单调递减,则实数a的取值范围是a≤﹣4.
其中正确的命题是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,定直线
,定直线![]() ,动点
,动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离之比等于
的距离之比等于![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设轨迹![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,过点
,过点![]() 作不与
作不与![]() 轴重合的直线交轨迹
轴重合的直线交轨迹![]() 于两点
于两点![]() ,直线
,直线![]() 分别交直线
分别交直线![]() 于点
于点![]() .试问:在
.试问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ?若存在,求出定点
?若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若以曲线![]() 上任意一点
上任意一点![]() 为切点作切线
为切点作切线![]() ,曲线上总存在异于
,曲线上总存在异于![]() 的点
的点![]() ,以点
,以点![]() 为切点作切线
为切点作切线![]() ,且
,且![]() ,则称曲线
,则称曲线![]() 具有“可平行性”,现有下列命题:
具有“可平行性”,现有下列命题:
①函数![]() 的图象具有“可平行性”;
的图象具有“可平行性”;
②定义在![]() 的奇函数
的奇函数![]() 的图象都具有“可平行性”;
的图象都具有“可平行性”;
③三次函数![]() 具有“可平行性”,且对应的两切点
具有“可平行性”,且对应的两切点![]() ,
, ![]() 的横坐标满足
的横坐标满足![]() ;
;
④要使得分段函数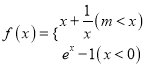 的图象具有“可平行性”,当且仅当
的图象具有“可平行性”,当且仅当![]() .
.
其中的真命题个数有()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实数m取什么数值时,复数z=m2﹣1+(m2﹣m﹣2)i分别是:
(1)实数;
(2)虚数;复数z=m2﹣1+(m2﹣m﹣2)i是虚数, ∴m2﹣m﹣2≠0
∴m≠﹣1.m≠2
(3)纯虚数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com