
【题目】如图,已知AB是半圆O的直径,O是半圆圆心,AB=8,M、N、P是将半圆圆周四等分的三个分点.
(1)从A、B、M、N、P这5个点中任取3个点,求这3个点组成等腰三角形的概率;
(2)在半圆内任取一点S,求△SOB的面积大于4 ![]() 的概率.
的概率.
【答案】
(1)
解:从A、B、M、N、P这5个点中任取3个点,一共可以组成10个三角形:△ABM、△ABN、△ABP、△AMN、△AMP、
△ANP、△BMN、△BMP、△BNP、△MNP,
其中是等腰三角形的只有△ABN、△ABN、△BN,△MNP,4个,
所以这3个点组成等腰三角形的概率P= ![]() .
.
(2)
解:连接MP,取线段MP的中点D,则OD⊥MP,
易求得OD=2 ![]() ,
,
当S点在线段MP上时,S△ABS= ![]() ×2
×2 ![]() ×4=4
×4=4 ![]() ,
,
所以只有当S点落在阴影部分时,三角形SAB面积才能大于4 ![]() ,而
,而
S阴影=S扇形OMP﹣S△OMP= ![]() ×
× ![]() ×42﹣
×42﹣ ![]() ×42=4π﹣8,
×42=4π﹣8,
所以由几何概型公式得三角形SAB的面积大于4 ![]() 的概率P=
的概率P= ![]() .
.

【解析】(1)这是古典概型,利用列举法进行求解即可.(2)是几何概型,求出对应区域的面积,结合几何概型的概率公式进行求解即可.
【考点精析】根据题目的已知条件,利用几何概型的相关知识可以得到问题的答案,需要掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.


科目:高中数学 来源: 题型:
【题目】对某商店一个月内每天的顾客人数进行统计,得到样本的茎叶图(如图所示).则该样本的中位数、众数、极差分别是( )
A.46 45 56
B.46 45 53
C.47 45 56
D.45 47 53
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,短轴右端点为
,短轴右端点为![]() ,
, ![]() 为线段
为线段![]() 的中点.
的中点.
(Ⅰ) 求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 任作一条直线与椭圆
任作一条直线与椭圆![]() 相交于两点
相交于两点![]() ,试探究在
,试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣mx+m,m、x∈R.
(1)若关于x的不等式f(x)>0的解集为R,求m的取值范围;
(2)若实x1 , x2数满足x1<x2 , 且f(x1)≠f(x2),证明:方程f(x)= ![]() [f(x1)+f(x2)]至少有一个实根x0∈(x1 , x2);
[f(x1)+f(x2)]至少有一个实根x0∈(x1 , x2);
(3)设F(x)=f(x)+1﹣m﹣m2 , 且|F(x)|在[0,1]上单调递增,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工某零件所花费的时间,为此做了四次实验,得到的数据如表:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;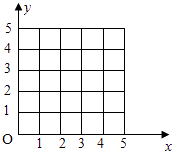
(2)求出y关于x的线性回归方程y= ![]() x+
x+ ![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工6个零件需要多少时间?
(注: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列命题:
①双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点;
有相同的焦点;
②“![]() ”是“2x2﹣5x﹣3<0”必要不充分条件;
”是“2x2﹣5x﹣3<0”必要不充分条件;
③“若xy=0,则x、y中至少有一个为0”的否命题是真命题.;
④若p是q的充分条件,r是q的必要条件,r是s的充要条件,则s是p的必要条件;
其中是真命题的有: .(把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+2sinα(α∈(0,![]() ))的导函数f′(x),若存在x0<1使得f′(x0)=f(x0)成立,则实数α的取值范围为( )
))的导函数f′(x),若存在x0<1使得f′(x0)=f(x0)成立,则实数α的取值范围为( )
A.(![]() ,
, ![]() )
)
B.(0,![]() )
)
C.(![]() ,
, ![]() )
)
D.(0,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示, ![]() 是某海湾旅游区的一角,其中
是某海湾旅游区的一角,其中![]() ,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸
,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸![]() 和
和![]() 上分别修建观光长廊
上分别修建观光长廊![]() 和AC,其中
和AC,其中![]() 是宽长廊,造价是
是宽长廊,造价是![]() 元/米,
元/米, ![]() 是窄长廊,造价是
是窄长廊,造价是![]() 元/米,两段长廊的总造价为120万元,同时在线段
元/米,两段长廊的总造价为120万元,同时在线段![]() 上靠近点
上靠近点![]() 的三等分点
的三等分点![]() 处建一个观光平台,并建水上直线通道
处建一个观光平台,并建水上直线通道![]() (平台大小忽略不计),水上通道的造价是
(平台大小忽略不计),水上通道的造价是![]() 元/米.
元/米.
(1) 若规划在三角形![]() 区域内开发水上游乐项目,要求
区域内开发水上游乐项目,要求![]() 的面积最大,那么
的面积最大,那么![]() 和
和![]() 的长度分别为多少米?
的长度分别为多少米?
(2) 在(1)的条件下,建直线通道![]() 还需要多少钱?
还需要多少钱?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com