
分析 (1)将两个方程都化为普通方程,C1与C2只有一个公共点,直线与圆相切,圆心到直线的距离等于半径,即可求实数m的值;
(2)求|OA|,|OB|,|OC|,利用△ABC的面积为3$\sqrt{3}$,即可求实数m(m<0)的值.
解答 解:(1)曲线C1的极坐标方程为ρ=4cosθ,即x2+y2=4x,即(x-2)2+y2=4;
曲线C2的参数方程为$\left\{\begin{array}{l}x=m+\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}$(t为参数),消去t可得y=$\sqrt{3}$(x-m).
∵C1与C2只有一个公共点,
∴直线与圆相切,
∴$\frac{|2\sqrt{3}-\sqrt{3}m|}{2}$=2,∴m=2±$\frac{4\sqrt{3}}{3}$;
(2)θ=$\frac{π}{3}$与C1交于点A(异于极点),|OA|=2,θ=$\frac{5π}{6}({ρ∈R})$与C1交于点B(异于极点),|OB|=2$\sqrt{3}$,
曲线C2的极坐标方程为ρ=$\frac{\sqrt{3}m}{2cos(θ+\frac{π}{6})}$,θ=$\frac{5π}{6}({ρ∈R})$,|OC|=$\frac{\sqrt{3}}{2}$m,
∴S△ABC=$\frac{1}{2}×2×$(2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$m)=3$\sqrt{3}$,∴m=-2.
点评 本题考查三种方程的互化,考查直线与圆的位置关系,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
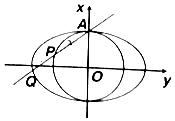 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),圆O:x2+y2=b2,过椭圆C的上顶点A的直线l:y=kx+b分别交圆O、椭圆C于不同的两点P、Q,设$\overrightarrow{AP}$=λ$\overrightarrow{PQ}$.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),圆O:x2+y2=b2,过椭圆C的上顶点A的直线l:y=kx+b分别交圆O、椭圆C于不同的两点P、Q,设$\overrightarrow{AP}$=λ$\overrightarrow{PQ}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$≤k≤2 | B. | k≤-$\frac{1}{2}$或k≥2 | C. | -2≤k≤$\frac{1}{2}$ | D. | k≤-2或k≥$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
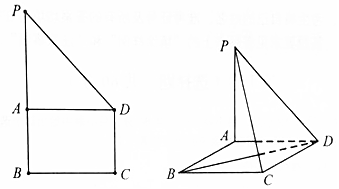 如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,点A在边PB上,AD∥BC,PB=3BC=6,现沿AD将△PAD折起,使平面PAD⊥平面ABCD.
如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,点A在边PB上,AD∥BC,PB=3BC=6,现沿AD将△PAD折起,使平面PAD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果α⊥β,那么α内一定存在直线平行于β | |
| B. | 如果α⊥γ,β⊥γ,α∩β=l,那么l⊥γ | |
| C. | 如果α不垂直于β,那么α内一定不存在直线垂直于β | |
| D. | 如果α⊥β,那么α内所有直线都垂直于β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{π}{2}$ | B. | $\frac{π}{2}$ | C. | 1 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com