
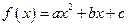
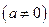 满足
满足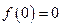 ,对于任意
,对于任意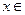 R都有
R都有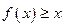 ,且
,且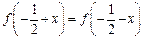 ,令
,令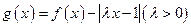 .
.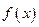 的表达式;
的表达式; 的单调区间;
的单调区间; 在区间
在区间 上的零点个数.
上的零点个数.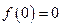 ,∴
,∴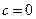 . … 1分
. … 1分 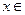 R都有
R都有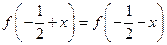 ,
,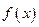 的对称轴为
的对称轴为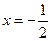 ,即
,即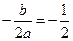 ,得
,得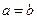 . …… 2分
. …… 2分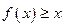 ,即
,即 对于任意
对于任意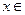 R都成立,∴
R都成立,∴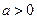 ,且
,且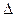
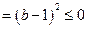 .
.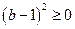 , ∴
, ∴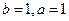 . ∴
. ∴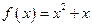 . …… 4分
. …… 4分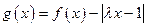
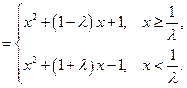 …… 5分
…… 5分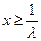 时,函数
时,函数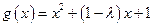 的对称轴为
的对称轴为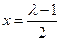 ,
, ,即
,即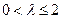 ,函数
,函数 在
在 上单调递增;…… 6分
上单调递增;…… 6分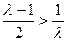 ,即
,即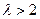 ,函数
,函数 在
在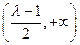 上单调递增,在
上单调递增,在 上单调递减.…… 7分
上单调递减.…… 7分 时,函数
时,函数 的对称轴为
的对称轴为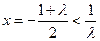 ,
, 在
在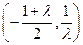 上单调递增,在
上单调递增,在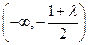 上单调递减.… 8分
上单调递减.… 8分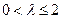 时,函数
时,函数 单调递增区间为
单调递增区间为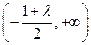 ,
,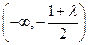 ; …… 9分
; …… 9分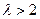 时,函数
时,函数 单调递增区间为
单调递增区间为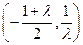 和
和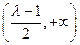 ,
,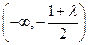 和
和 .… 10分
.… 10分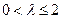 时,由(2)知函数
时,由(2)知函数 在区间
在区间 上单调递增,
上单调递增,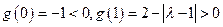 ,
, 在区间
在区间 上只有一个零点. …… 11分
上只有一个零点. …… 11分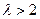 时,则
时,则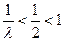 ,而
,而
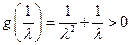 ,
, ,
, ,由于
,由于 ,
,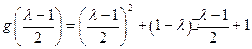
 ,
, 在区间
在区间 上只有一个零点; 12分
上只有一个零点; 12分 ,由于
,由于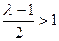 且
且
 ,此时,函数
,此时,函数 在区间
在区间
 时,函数
时,函数 在区间
在区间 上只有一个零点;
上只有一个零点; 时,函数
时,函数 在区间
在区间 上有两个不同的零点. …… 14分
上有两个不同的零点. …… 14分

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com