【答案】
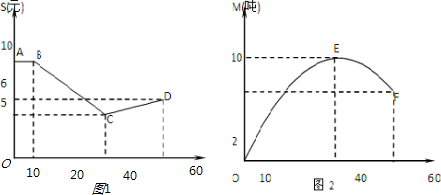
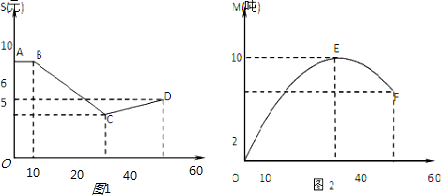
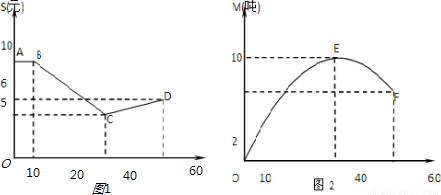
分析:(1)根据图1,发现当0≤t≤10时,函数S(t)=10,而当10<t≤40时和当40<t≤60时,函数S(t)的表达式都是一次函数,可以先设出它们的一次解析式,利用图象上的已知点求出一次项系数和常数项,可以得到函数S(t)的函数关系式.对于M(t),根据它的图象是开口向下的抛物线,经过原点且关于直线t=40对称,结合顶点坐标,不难用待定系数的方法求出M(t)关于t的函数关系式;
(2)根据(1)的函数S(t)的分段函数关系式,分①当0≤t≤10时,②当10<t≤40时,③当40<t≤60时,分别得到P(t)关于t的函数关系式,利用导数工具讨论各段上的单调性,从而得出函数P(t)在各段上的最大值,再将各个最大值进行比较,从而得出当t=47时,水果市场的销售额最大.
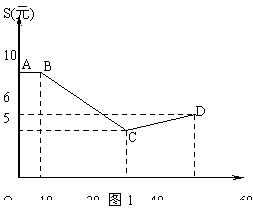
解答:解:(1)①由图1可知,当0≤t≤10时,S(t)=10
②当10<t≤40时,设S(t)=a
1t+b
1,因为函数S(t)的图象过点B(10,10),C(40,5)
所以
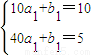
,解之得

∴当10<t≤40时,S(t)=
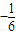
t+
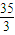
③当40<t≤60时,设S(t)=a
2t+b
2,因为函数S(t)的图象过点C(40,5),C(60,6),
所以用类似②的方法可得
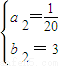
,此时S(t)=
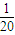
t+3,
综上所述,S(t)=
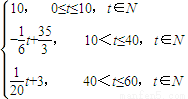
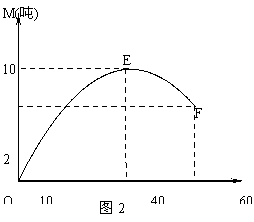
由图2可知,函数M(t)在x=40时取得最大值,故设M(t)=a(t-40)
2+10
又函数M(t)的图象过点O(0,0),所以a(-40)
2+10=0,解之得a=-
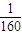
所以M(t)=-
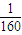
(t-40)
2+10=-
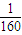
t
2+

t,0≤t≤160,t∈N
(2)在这60天内,设该水果市场的销售额与天天数的函数关系为P(t),则
①当0≤t≤10,t∈N时,P(t)=1000S(t)M(t)=10000(-
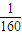
t
2+

t)
可得:当t=10时,P(t)
max=P(10)=43750.
②当10<t≤40,t∈N时,P(t)=1000S(t)M(t)=1000(-

t+
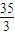
)(-
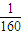
t
2+

t)=
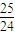
(t
3-150t
2+5600t)
∵(t
3-150t
2+5600t)′=3t
2-300t+5600=3(t-50)
2-1900>0在区间(10,24]上成立,
且(t
3-150t
2+5600t)′=3t
2-300t+5600=3(t-50)
2-1900<0在区间[25,40]上成立
∴P(t)在区间(10,24]上是单调增函数,在区间[25,40]上是单调减函数
当10<t≤40,t∈N时,P(t)
max应该是P(24)和P(25)中的较大者
而P(24)=64400,P(25)≈64453.13,因此P(t)
max=P(25)
③当40<t≤60,t∈N时,P(t)=1000S(t)M(t)=1000(
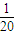
t+3)(-
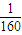
t
2+

t)=
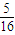
(-t
3+20t
2+4800t)
用类似②的方法,可得P(t)在区间(40,47]上是单调增函数,在区间[48,60]上是单调减函数.
而P(47)≈51861.56>P(48)=51840,所以此时P(t)
max=P(47)
综上所述,P(t)的最大值为P(47)≈51861.56
所以在这60天内,该水果市场第47天的销售额最大.
点评:本题以一个实际问题为例,考查了分段函数的单调性与最值的知识点,计算量很大,是一道难题.在解题过程中用到了分类讨论与转化化归的思想,综合了函数多种性质加以解决.

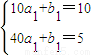 ,解之得
,解之得
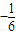 t+
t+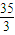
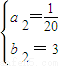 ,此时S(t)=
,此时S(t)=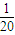 t+3,
t+3,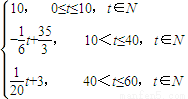
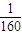
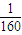 (t-40)2+10=-
(t-40)2+10=-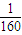 t2+
t2+ t,0≤t≤160,t∈N
t,0≤t≤160,t∈N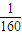 t2+
t2+ t)
t) t+
t+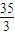 )(-
)(-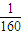 t2+
t2+ t)=
t)=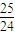 (t3-150t2+5600t)
(t3-150t2+5600t)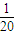 t+3)(-
t+3)(-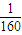 t2+
t2+ t)=
t)=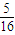 (-t3+20t2+4800t)
(-t3+20t2+4800t)

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案