
【题目】某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第1组[157.5,162.5),第2组[162.5,167.5),…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图. 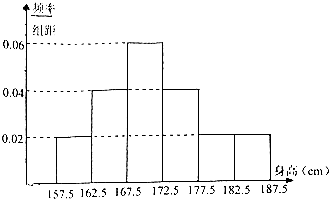
(1)试评估该校高三年级男生的平均身高;
(2)求这50名男生身高在177.5cm以上(含177.5cm)的人数;
(3)在这50名男生身高在177.5cm以上(含177.5cm)的人中任意抽取2人,该2人中身高排名(从高到低)在全省前130名的人数记为ξ,求ξ的分布列和数学期望.
参考数据:若ξ~N(μ,σ2),则P(μ﹣σ<ξ≤μ+σ)=0.6826,P(μ﹣2σ<ξ≤μ+2σ)=0.9544,P(μ﹣3σ<ξ≤μ+3σ)=0.9974.
【答案】
(1)解:根据频率分布直方图,得我校高三年级男生平均身高为 ![]() =160×0.02×5+165×0.04×5+170×0.06×5+175×0.04×5+180×0.02×5+185×0.02×5=171.5,
=160×0.02×5+165×0.04×5+170×0.06×5+175×0.04×5+180×0.02×5+185×0.02×5=171.5,
∴高于全市的平均值170.5;
(2)解:由频率分布直方图知,后两组频率为0.2,
∴人数为0.2×50=10,
即这50名男生身高在177.5cm以上(含177.5 cm)的人数为10人;
(3)解:∵P(170.5﹣3×4<ξ≤170.5+3×4)=0.9974,
∴P(ξ≥182.5)= ![]() =0.0013,
=0.0013,
∴0.0013×100 000=130,
全省前130名的身高在182.5 cm以上,这50人中182.5 cm以上的有5人;
∴随机变量ξ可取0,1,2,于是
P(ξ=0)= ![]() =
= ![]() ,P(ξ=1)=
,P(ξ=1)= ![]() =
= ![]() ,P(ξ=2)=
,P(ξ=2)= ![]() =,
=,
∴Eξ=0× ![]() +1×
+1× ![]() +2×
+2× ![]() =1.
=1.
【解析】(1)计算平均身高用组中值×频率,即可得到结论;(2)先理解频率分布直方图横纵轴表示的意义,横轴表示身高,纵轴表示频数,即每组中包含个体的个数;
根据频数分布直方图,了解数据的分布情况,知道每段所占的比例,从而求出这50名男生身高在177.5cm以上(含177.5cm)的人数;(III)先根据正态分布的规律求出全市前130名的身高在182.5cm以上的50人中的人数,确定ξ的可能取值,求出其概率,即可得到ξ的分布列与期望.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息,以及对离散型随机变量及其分布列的理解,了解在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣2ax+1+b(a>0)
(1)若f(x)在区间[2,3]上的最大值为4、最小值为1,求a,b的值;
(2)若a=1,b=1,关于x的方程f(|2x﹣1|)+k(4﹣3|2x﹣1|)=0,有3个不同的实数解,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在△ABC中,已知AB=15,BC=14,CA=13.将△ABC沿BC边上的高AD折成一个如图②所示的四面体A﹣BCD,使得图②中的BC=11. 
(1)求二面角B﹣AD﹣C的平面角的余弦值;
(2)在四面体A﹣BCD的棱AD上是否存在点P,使得 ![]() =0?若存在,请指出点P的位置;若不存在,请给出证明.
=0?若存在,请指出点P的位置;若不存在,请给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两个随机变量x,y的取值表为
x | 0 | 1 | 3 | 4 |
y | 2.2 | 4.3 | 4.8 | 6.7 |
若x,y具有线性相关关系,且 ![]() =
= ![]() x+2.6,则下列四个结论错误的是( )
x+2.6,则下列四个结论错误的是( )
A.x与y是正相关
B.当x=6时,y的估计值为8.3
C.x每增加一个单位,y增加0.95个单位
D.样本点(3,4.8)的残差为0.56
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )
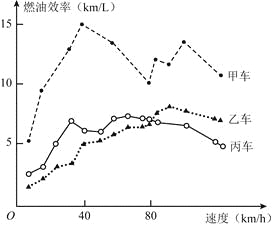
A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 与点
与点![]() 的距离比它的直线
的距离比它的直线![]() 的距离小2.
的距离小2.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)![]() 是点
是点![]() 轨迹上互相垂直的两条弦,问:直线
轨迹上互相垂直的两条弦,问:直线![]() 是否经过
是否经过![]() 轴上一定点,若经过,求出该点坐标;若不经过,说明理由.
轴上一定点,若经过,求出该点坐标;若不经过,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位建立坐标系,已知直线l的极坐标方程为2ρcosθ+ρsinθ=3,曲线C的参数方程为 ![]() (α为参数).
(α为参数).
(1)求曲线C的普通方程和直线l的直角坐标方程;
(2)P(1,1),设直线l与曲线C相交于A、B两点,求|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]()
![]() ,
,![]()
(1)若![]() ,且对
,且对![]() ,函数
,函数![]() 的值域为
的值域为![]() ,求
,求![]() 的表达式;
的表达式;
(2)在(1)的条件下,函数![]() 在
在![]() 上单调递减,求实数
上单调递减,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,
,![]() ,
,![]() 且
且![]() 为偶函数,证明
为偶函数,证明![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l:x-y-2=0,抛物线C:y2=2px(p>0).

(1)若直线l过抛物线C的焦点,求抛物线C的方程;
(2)当p=1时,若抛物线C上存在关于直线l对称的相异两点P和Q.求线段PQ的中点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com