
【题目】已知动点M到定点F1(-2,0)和F2(2,0)的距离之和为![]() .
.
(1)求动点M的轨迹C的方程;
(2)设N(0,2),过点P(-1,-2)作直线l,交曲线C于不同于N的两点A,B,直线NA,NB的斜率分别为k1,k2,求k1+k2的值.
【答案】(1)![]() ;(2)4
;(2)4
【解析】
本题考查椭圆的基本量间的关系及韦达定理的应用
(1)考查椭圆的基本量间的关系
(2)是直线与椭圆相交于![]() 两点,先设出
两点,先设出![]() 两点坐标,本题的突破口是在消参后的方程中找出两根之和、两根之积,整理斜率的表达式,在本问中需考虑直线的斜率是否存在
两点坐标,本题的突破口是在消参后的方程中找出两根之和、两根之积,整理斜率的表达式,在本问中需考虑直线的斜率是否存在
解:(1)由椭圆的定义,可知点M的轨迹是以F1,F2为焦点,![]() 为长轴长的椭圆.
为长轴长的椭圆.
由c=2,a=2![]() ,得b=2.
,得b=2.
故动点M的轨迹C的方程为![]() .
.
(2)当直线l的斜率存在时,设其方程为y+2=k(x+1),
由 得(1+2k2)x2+4k(k-2)x+2k2-8k=0.
得(1+2k2)x2+4k(k-2)x+2k2-8k=0.
Δ=[4k(k-2)]2-4(1+2k2)(2k2-8k)>0,则k>0或k<-![]()
设A(x1,y1),B(x2,y2),则 ![]() ,
, ![]() .
.
从而![]()
![]()
![]()
当直线l的斜率不存在时,得
所以k1+k2=4.
综上,恒有k1+k2=4.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中,![]() ,且点
,且点![]() (
(![]() )在直线
)在直线![]() 上.
上.
(1)求数列![]() 的通项公式;
的通项公式;
(2)对任意的![]() ,将数列
,将数列![]() 落入区间
落入区间![]() 内的项的个数记为
内的项的个数记为![]() ,求
,求![]() 的通项公式;
的通项公式;
(3)对于(2)中![]() ,记
,记![]() ,数列
,数列![]() 前
前![]() 项和为
项和为![]() ,求使等式
,求使等式![]() 成立的所有正整数
成立的所有正整数![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《流浪地球》是由刘慈欣的科幻小说改编的电影,在2019年春节档上影,该片上影标志着中国电影科幻元年的到来;为了振救地球,延续百代子孙生存的希望,无数的人前仆后继,奋不顾身的精神激荡人心,催人奋进.某网络调查机构调查了大量观众的评分,得到如下统计表:
评分 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
频率 | 0.03 | 0.02 | 0.02 | 0.03 | 0.04 | 0.05 | 0.08 | 0.15 | 0.21 | 0.36 |
(1)求观众评分的平均数?
(2)视频率为概率,若在评分大于等于8分的观众中随机地抽取1人,他的评分恰好是10分的概率是多少?
(3)视频率为概率,在评分大于等于8分的观众中随机地抽取4人,用![]() 表示评分为10分的人数,求
表示评分为10分的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线![]() 上的动点
上的动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离相等.
的距离相等.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 分别作射线
分别作射线![]() 、
、![]() 交曲线
交曲线![]() 于不同的两点
于不同的两点![]() 、
、![]() ,且以
,且以![]() 为直径的圆经过点
为直径的圆经过点![]() .试探究直线
.试探究直线![]() 是否过定点?如果是,请求出该定点;如果不是,请说明理由.
是否过定点?如果是,请求出该定点;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .数列
.数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)写出一个正整数![]() ,使得
,使得![]() 是数列
是数列![]() 的项;
的项;
(3)设数列![]() 的通项公式为
的通项公式为![]() ,问:是否存在正整数
,问:是否存在正整数![]() 和
和![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列?若存在,请求出所有符合条件的有序整数对
成等差数列?若存在,请求出所有符合条件的有序整数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,椭圆
,椭圆![]() 的短半轴长等于圆
的短半轴长等于圆![]() 的半径,且过
的半径,且过![]() 右焦点的直线与圆
右焦点的直线与圆![]() 相切于点
相切于点 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若动直线![]() 与圆
与圆![]() 相切,且与
相切,且与![]() 相交于
相交于![]() 两点,求点
两点,求点![]() 到弦
到弦![]() 的垂直平分线距离的最大值.
的垂直平分线距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是一块边长为7米的正方形铁皮,其中
是一块边长为7米的正方形铁皮,其中![]() 是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮
是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮![]() ,其中P是
,其中P是![]() 上一点.设
上一点.设![]() ,长方形
,长方形![]() 的面积为S平方米.
的面积为S平方米.

(1)求S关于![]() 的函数解析式;
的函数解析式;
(2)设![]() ,求S关于t的表达式以及S的最大值.
,求S关于t的表达式以及S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知AB是圆O的直径,C,D是圆上不同两点,且![]() ,
,![]() ,
,![]() 圆O所在平面.
圆O所在平面.
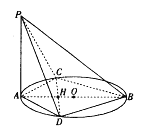
(1)求直线PB与CD所成角;
(2)若PB与圆O所在平面所成角为![]() ,且
,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com