
【题目】数列{an}中,定义:dn=an+2+an﹣2an+1(n≥1),a1=1.
(1)若dn=an , a2=2,求an;
(2)若a2=﹣2,dn≥1,求证此数列满足an≥﹣5(n∈N*);
(3)若|dn|=1,a2=1且数列{an}的周期为4,即an+4=an(n≥1),写出所有符合条件的{dn}.
【答案】
(1)解:∵an=dn=an+2+an﹣2an+1(n≥1),
∴an+2﹣2an+1=0(n≥1);
又∵a1=1,a2=2,
∴数列是以1为首项,2为公比的等比数列,
故数列{an}的通项公式为 ![]() ;
;
(2)解:证明:∵dn≥1,
∴an+2+an﹣2an+1≥1,
令cn=an+1﹣an,则
cn+1﹣cn≥1,
叠加得,cn≥n﹣4;
即an+1﹣an≥n﹣4,
叠加可得, ![]() ≥﹣5.
≥﹣5.
(3)解:由于|dn|=1,a1=1,a2=1,
若d1=1,则可得a3=2,
若d1=﹣1可得a3=0;
同理,若d2=1可得a4=4或a4=2,
若d2=﹣1可得a4=0或a4=﹣2;
具体如下表所示,
1,1, 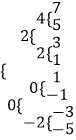 ;
;
所以{an}可以为1,1,2,2;1,1,2,2;1,1,2,2;…
或1,1,0,0;1,1,0,0;1,1,0,0;…
此时相应的{dn}为1,﹣1,﹣1,1,1,﹣1,﹣1,1,…
或﹣1,1,1,﹣1,﹣1,1,1,﹣1,….
【解析】(1)化简可得an+2﹣2an+1=0(n≥1);从而检验可得数列是以1为首项,2为公比的等比数列,从而求得;(2)由dn≥1,构造cn=an+1﹣an , 从而可得cn+1﹣cn≥1,从而可得an+1﹣an≥n﹣4,从而可得 ![]() ≥﹣5.(Ⅲ)由|dn|=1,a1=1,a2=1讨论求a3 , a4 , a5 , 从而归纳可得.
≥﹣5.(Ⅲ)由|dn|=1,a1=1,a2=1讨论求a3 , a4 , a5 , 从而归纳可得.
【考点精析】本题主要考查了数列的通项公式的相关知识点,需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】《九章算术》中有“今有五人分无钱,令上二人所得与下三人等,问各得几何?”.其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱?”这个问题中,甲所得为( )
A.![]() 钱
钱
B.![]() 钱
钱
C.![]() 钱
钱
D.![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() 具有性质
具有性质![]() :对任意的
:对任意的![]()
![]() ,
,![]() ,使得
,使得![]() 成立.
成立.
(Ⅰ)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(Ⅱ)求证![]() ;
;
(Ⅲ)若![]() ,求数集
,求数集![]() 中所有元素的和的最小值.
中所有元素的和的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形∠CAB=90°,AC=2a,E,F分别为AC,BC的中点,沿EF将△CEF折起,得到如图2所示的四棱锥C′﹣ABFE
(1)求证:AB⊥平面AEC′;
(2)当四棱锥C′﹣ABFE体积取最大值时,
①若G为BC′中点,求异面直线GF与AC′所成角;
②在C′﹣ABFE中AE交BF于C,求二面角A﹣CC′﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某镇有一块空地![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 。当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖
。当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖![]() ,其中
,其中![]() 都在边
都在边![]() 上,且
上,且![]() ,挖出的泥土堆放在
,挖出的泥土堆放在![]() 地带上形成假山,剩下的
地带上形成假山,剩下的![]() 地带开设儿童游乐场. 为安全起见,需在
地带开设儿童游乐场. 为安全起见,需在![]() 的周围安装防护网.
的周围安装防护网.
(1)当![]() 时,求防护网的总长度;
时,求防护网的总长度;
(2)若要求挖人工湖用地![]() 的面积是堆假山用地
的面积是堆假山用地![]() 的面积的
的面积的![]() 倍,试确定
倍,试确定![]() 的大小;
的大小;
(3)为节省投入资金,人工湖![]() 的面积要尽可能小,问如何设计施工方案,可使
的面积要尽可能小,问如何设计施工方案,可使![]() 的面积最小?最小面积是多少?
的面积最小?最小面积是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sin(
sin( ![]() ωx)cos(
ωx)cos( ![]() ωx)+2cos2(
ωx)+2cos2( ![]() ωx)(ω>0),且函数f(x)的最小正周期为π.
ωx)(ω>0),且函数f(x)的最小正周期为π.
(1)求ω的值;
(2)求f(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1 , C2的极坐标方程分别为ρ=2cosθ, ![]() ,射线θ=φ,
,射线θ=φ, ![]() ,
, ![]() 与曲线C1交于(不包括极点O)三点A,B,C.
与曲线C1交于(不包括极点O)三点A,B,C.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)当 ![]() 时,求点B到曲线C2上的点的距离的最小值.
时,求点B到曲线C2上的点的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点P(0,1)在圆C:x2+y2+2mx﹣2y+m2﹣4m+1=0内,若存在过点P的直线交圆C于A、B两点,且△PBC的面积是△PAC的面积的2倍,则实数m的取值范围为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com