
【题目】用![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这六个数字.
这六个数字.
(![]() )能组成多少个无重复数字的四位偶数.
)能组成多少个无重复数字的四位偶数.
(![]() )能组成多少个比
)能组成多少个比![]() 大的四位数.
大的四位数.
【答案】(1)156(2)270
【解析】分析:(1)按0是否在个位分类讨论,再根据分类加法计数原理求结果,(2)根据首位数分三类,第一类为2,3,4,5;第二类形如![]() ,
,![]() ,第三类为形如
,第三类为形如![]() ,
,![]() ,再根据分类加法计数原理求结果.
,再根据分类加法计数原理求结果.
详解:解:(![]() )符合要求的四位偶数可分为三类:
)符合要求的四位偶数可分为三类:
第一类:![]() 在个位时,有
在个位时,有![]() 个.
个.
第二类:![]() 在个位时,首位从
在个位时,首位从![]() ,
,![]() ,
,![]() ,
,![]() 中选定
中选定![]() 个,有
个,有![]() 种可能,十位和百位从余下的数字中选取有
种可能,十位和百位从余下的数字中选取有![]() 种可能,于是有
种可能,于是有![]() 个.
个.
第三类,![]() 在个位时,同第二类,也有
在个位时,同第二类,也有![]() 个.
个.
由分类加法计数原理可知,四位偶数共有:![]() 个.
个.
(![]() )符合要求的比
)符合要求的比![]() 大的四位数可分为三类:
大的四位数可分为三类:
第一类:形如![]() ,
,![]() ,
,![]() ,
,![]() ,这样的数共
,这样的数共![]() 个.
个.
第二类:形如![]() ,
,![]() ,共有
,共有![]() 个.
个.
第三类:形如![]() ,
,![]() ,共
,共![]() 个.
个.
由分类加法计数原理可知,比![]() 大的四位数共有
大的四位数共有![]() 个.
个.


科目:高中数学 来源: 题型:
【题目】某人承揽一项业务,需做文字标牌4个,绘画标牌5个,现有两种规格的原料,甲种规格每张3m2,可做文字标牌1个,绘画标牌2个,乙种规格每张2m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张,才能使总的用料面积最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
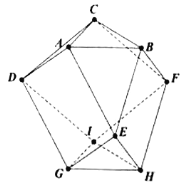
【题目】在如图所示的十一面体![]() 中,用
中,用![]() 种不同颜色给这个几何体各个顶点染色,每个顶点染一种颜色,要求每条棱的两端点异色,则不同的染色方案种数为__________.
种不同颜色给这个几何体各个顶点染色,每个顶点染一种颜色,要求每条棱的两端点异色,则不同的染色方案种数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在(﹣∞,0)上的可导函数,其导函数为f′(x),且有xf′(x)>x2+3f(x),则不等式8f(x+2014)+(x+2014)3f(﹣2)>0的解集为( )
A.(﹣∞,﹣2016)
B.(﹣2018,﹣2016)
C.(﹣2018,0)
D.(﹣∞,﹣2018)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50名学生在一次百米测试中,成绩全部介于13 s与19 s之间,将测试结果分成如下六组:[13,14),[14,15),[15,16),[16,17),[17,18),[18,19].如图是按上述分组方法得到的频率分布直方图,设成绩小于17 s的学生人数占全班人数的百分比为x,成绩在[15,17)中的学生人数为y,则从频率分布直方图中可以分析出x和y分别为 ( )
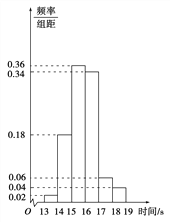
A. 90%,35B. 90%,45
C. 10%,35D. 10%,45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出![]() (万元)与销售
(万元)与销售![]() (万元)之间有如下的对应数据:
(万元)之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
若由资料可知![]() 对
对![]() 呈线性相关关系,试求:
呈线性相关关系,试求:
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)据此估计广告费用支出为10万元时销售收入![]() 的值.
的值.
(参考公式:
 ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于 x 的函数f(x)=lg(x2﹣2x﹣3)的定义域为集合 A,函数 g(x)=x﹣a,(0≤x≤4)的值域为集合 B.
(1)求集合 A,B;
(2)若集合 A,B 满足 A∩B=B,求实数 a 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】意大利著名数学家斐波那契在研究兔子的繁殖问题时,发现有这样的一列数:1,1,2,3,5,8,…,该数列的特点是:前两个数均为1,从第三个数起,每一个数都等于它前面两个数的和.人们把这样的一列数组成的数列{an}称为斐波那契数列,则 ![]() ﹣
﹣ ![]() =( )
=( )
A.0
B.﹣1
C.1
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com