
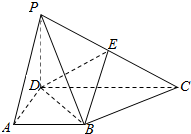
 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.分析 (1)证明PD⊥平面ABCD,推出PD⊥BC,BD⊥BC,然后证明BC⊥平面PBD.
(2)过E作EF∥PD交DC于F,EF⊥平面ABCD,求出$EF=\frac{4}{3}$,利用VP-BDE=VP-BCD-VE-BCD,求解即可.
解答 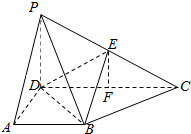 (1)证:∵PD⊥CD,平面PCD⊥平面ABCD,平面PCD与平面ABCD相交于CD
(1)证:∵PD⊥CD,平面PCD⊥平面ABCD,平面PCD与平面ABCD相交于CD
∴PD⊥平面ABCD,∴PD⊥BC(2分)
在△ABD中,∠A=90°,AB=AD=2,∴$BD=2\sqrt{2}$,∠ADB=45°
在△ABD中,∠BDC=45°,$BD=2\sqrt{2}$,DC=4
∴$cos45°=\frac{{B{D^2}+D{C^2}-B{C^2}}}{2BD•DC}⇒BC=2\sqrt{2}$
由BD2+BC2=16=DC2知BD⊥BC(4分)
∵PD⊥BC,BD、PD相交于D,∴BC⊥平面PBD(6分)
(2)解:过E作EF∥PD交DC于F,由(1)知EF⊥平面ABCD
由CE=2PE得:$\frac{EF}{PD}=\frac{CE}{PC}=\frac{2}{3}$,∴$EF=\frac{4}{3}$(8分)${V_{P-BDE}}={V_{P-BCD}}-{V_{E-BCD}}=\frac{1}{3}PD•{S_{△BCD}}-\frac{1}{3}EF•{S_{△BCD}}=\frac{2}{9}{S_{△BCD}}$(10分)${S_{△BCD}}=\frac{1}{2}CD•AD=\frac{1}{2}×4×2=4$
∴${V_{P-BDE}}=\frac{8}{9}$(12分)
点评 本题考查几何体的体积,以及直线与平面垂直的判定定理的应用,考查转化思想以及空间想象能力计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)<f(b)<f(c) | B. | f(c)<f(b)<f(a) | C. | f(c)<f(a)<f(b) | D. | f(b)<f(a)<f(c) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,5) | B. | (-2,2) | C. | (-$\sqrt{7}$,$\sqrt{7}$) | D. | (-$\sqrt{3}$,$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 2或3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
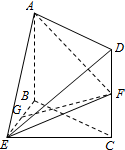 如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G是线段BE的中点,点F在线段CD上且GF∥平面ADE.
如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G是线段BE的中点,点F在线段CD上且GF∥平面ADE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com