
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,并解答.已知等差数列
这三个条件中任选一个,补充在下面问题中,并解答.已知等差数列![]() 的公差
的公差![]() ,前
,前![]() 项和为
项和为![]() ,若_______,数列
,若_______,数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)求![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)选①:![]() ;选②:
;选②:![]() ;选③:
;选③:![]() ;(2)选①:
;(2)选①:![]() ;选②:
;选②:![]() ;选③:
;选③:![]()
【解析】
若选①:(1)先令![]() ,代入
,代入![]() 求出
求出![]() ,再由
,再由![]() 求出公差
求出公差![]() ,进而求出
,进而求出![]() ;
;
(2)先由(1)中求出的![]() 结合
结合![]() 得到
得到![]() ,再求
,再求![]() .
.
若选②:(1)先令![]() ,代入
,代入![]() 求出
求出![]() ,再由
,再由![]() ,
,![]() ,求出公差
,求出公差![]() ,进而求出
,进而求出![]() ;
;
(2)先由(1)中求出的![]() 结合
结合![]() 得到
得到![]() ,再求
,再求![]() .
.
若选③:(1)(1)先令![]() ,代入
,代入![]() 求出
求出![]() ,再由
,再由![]() 求出公差
求出公差![]() ,进而求出
,进而求出![]() ;
;
(2)先由(1)中求出的![]() 结合
结合![]() 得到
得到![]() ,再求
,再求![]() .
.
若选①:
(1)![]() ,
,![]() 当
当![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
又![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)由(1)知:![]() ,即
,即![]() ,
,![]() ,
,
又![]() ,
,![]() 数列
数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列,
为公比的等比数列,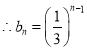 ,
,
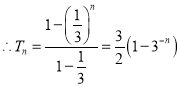 .
.
若选②:
(1)![]() ,
,![]() 当
当![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
又![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)由(1)知:![]() ,即
,即![]() ,
,![]() ,
,
又![]() ,
,![]() 数列
数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列,
为公比的等比数列,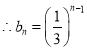 ,
,
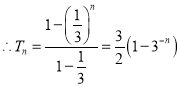 .
.
若选③:
(1)![]() ,
,![]() 当
当![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
又![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)由(1)知:![]() ,即
,即![]() ,
,![]() ,
,
又![]() ,
,![]() 数列
数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列,
为公比的等比数列,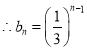 ,
,
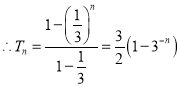 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线
的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线![]() :
: ![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
(Ⅰ)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(Ⅱ)设![]() 是坐标原点,直线
是坐标原点,直线![]() 平行于
平行于![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且与直线
,且与直线![]() 交于点
交于点![]() ,证明:存在常数
,证明:存在常数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年寒假期间新冠肺炎肆虐,全国人民众志成城抗击疫情.某市要求全体市民在家隔离,同时决定全市所有学校推迟开学.某区教育局为了让学生“停课不停学”,要求学校各科老师每天在网上授课,每天共280分钟,请学生自主学习.区教育局为了了解高三学生网上学习情况,上课几天后在全区高三学生中采取随机抽样的方法抽取了100名学生进行问卷调查,为了方便表述把学习时间在![]() 分钟的学生称为
分钟的学生称为![]() 类,把学习时间在
类,把学习时间在![]() 分钟的学生称为
分钟的学生称为![]() 类,把学习时间在
类,把学习时间在![]() 分钟的学生称为
分钟的学生称为![]() 类,随机调查的100名学生学习时间的人数频率分布直方图如图所示:以频率估计概率回答下列问题:
类,随机调查的100名学生学习时间的人数频率分布直方图如图所示:以频率估计概率回答下列问题:

(1)求100名学生中![]() ,
,![]() ,
,![]() 三类学生分别有多少人?
三类学生分别有多少人?
(2)在![]() ,
,![]() ,
,![]() 三类学生中,按分层抽样的方法从上述100个学生中抽取10人,并在这10人中任意邀请3人电话访谈,求邀请的3人中是
三类学生中,按分层抽样的方法从上述100个学生中抽取10人,并在这10人中任意邀请3人电话访谈,求邀请的3人中是![]() 类的学生人数的分布列和数学期望;
类的学生人数的分布列和数学期望;
(3)某校高三(1)班有50名学生,某天语文和数学老师计划分别在19:00—19:40和20:00—20:40在线上与学生交流,由于受校园网络平台的限制,每次只能30个人同时在线学习交流.假设这两个时间段高三(1)班都有30名学生相互独立地随机登录参加学习交流.设![]() 表示参加语文或数学学习交流的人数,当
表示参加语文或数学学习交流的人数,当![]() 为多少时,其概率最大.
为多少时,其概率最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
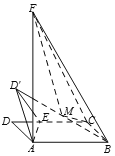
【题目】如图,已知矩形ABCD,![]() ,
,![]() ,AF⊥平面ABC,且
,AF⊥平面ABC,且![]() .E为线段DC上一点,沿直线AE将△ADE翻折成
.E为线段DC上一点,沿直线AE将△ADE翻折成![]() ,M为
,M为![]() 的中点,则三棱锥
的中点,则三棱锥![]() 体积的最小值是________.
体积的最小值是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 存在极值,求实数a的取值范围;
存在极值,求实数a的取值范围;
(2)设![]() ,设
,设![]() 是定义在
是定义在![]() 上的函数.
上的函数.
(ⅰ)证明:![]() 在
在![]() 上为单调递增函数(
上为单调递增函数(![]() 是
是![]() 的导函数);
的导函数);
(ⅱ)讨论![]() 的零点个数.
的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() 为等差数列
为等差数列 ![]() 的前
的前 ![]() 项和,其中
项和,其中 ![]() ,且
,且 ![]() .
.
(1)求常数 ![]() 的值,并写出
的值,并写出 ![]() 的通项公式;
的通项公式;
(2)记 ![]() ,数列
,数列 ![]() 的前
的前 ![]() 项和为
项和为 ![]() ,若对任意的
,若对任意的 ![]() ,都有
,都有 ![]() ,求常数
,求常数 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秉承“绿水青山就是金山银山”的发展理念,某市环保部门通过制定评分标准,先对本市50%的企业进行评估,评出四个等级,并根据等级给予相应的奖惩,如下表所示:
评估得分 |
|
|
|
|
评定等级 | 不合格 | 合格 | 良好 | 优秀 |
奖励(万元) |
| 20 | 40 | 80 |
(1)环保部门对企业抽查评估完成后,随机抽取了50家企业的评估得分(![]() 分)为样本,得到如下频率分布表:
分)为样本,得到如下频率分布表:
评估得分 |
|
|
|
|
|
|
频率 | 0.04 | 0.10 |
|
| 0.20 | 0.12 |
其中![]() 、
、![]() 表示模糊不清的两个数字,但知道样本评估得分的平均数是73.6.现从样本外的数百个企业评估得分中随机抽取3个,若以样本中频率为概率,求至少有两家企业的奖励不少于40万元的概率;
表示模糊不清的两个数字,但知道样本评估得分的平均数是73.6.现从样本外的数百个企业评估得分中随机抽取3个,若以样本中频率为概率,求至少有两家企业的奖励不少于40万元的概率;
(2)某企业为取得一个好的得分,在评估前投入80万元进行技术改造,由于技术水平问题,被评定为“合格”“良好”和“优秀”的概率分别为![]() ,
,![]() 和
和![]() ,且由此增加的产值分别为20万元,40万元和60万元.设该企业当年因改造而增加的利润为
,且由此增加的产值分别为20万元,40万元和60万元.设该企业当年因改造而增加的利润为![]() 万元,求
万元,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com