
已知函数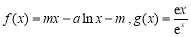 ,其中m,a均为实数.
,其中m,a均为实数.
(1)求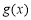 的极值;
的极值;
(2)设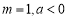 ,若对任意的
,若对任意的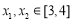
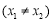 ,
,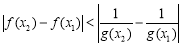 恒成立,求
恒成立,求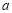 的最小值;
的最小值;
(3)设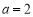 ,若对任意给定的
,若对任意给定的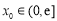 ,在区间
,在区间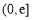 上总存在
上总存在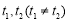 ,使得
,使得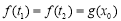 成立,求
成立,求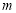 的取值范围.
的取值范围.
(1)极大值为1,无极小值.(2)3 ? .(3)
.(3) .
.
【解析】
试题分析:(1)求函数极值,先明确定义域为 再求其导数为
再求其导数为 .由
.由 ,得x = 1.分析导数在定义区间符号正负,确定函数先增后减,所以y =
,得x = 1.分析导数在定义区间符号正负,确定函数先增后减,所以y = 有极大值为1,无极小值.(2)不等式恒成立问题,先化简不等式
有极大值为1,无极小值.(2)不等式恒成立问题,先化简不等式 .化简不等式的难点有两个,一是绝对值,二是两个参量
.化简不等式的难点有两个,一是绝对值,二是两个参量 可从函数单调性去绝对值,分析两个函数,一是
可从函数单调性去绝对值,分析两个函数,一是 ,二是
,二是 .利用导数可知两者都是增函数,故原不等式等价于
.利用导数可知两者都是增函数,故原不等式等价于 ,变量分离调整为
,变量分离调整为 ,这又等价转化为函数
,这又等价转化为函数 在区间
在区间 上为减函数,即
上为减函数,即 在
在 上恒成立.继续变量分离得
上恒成立.继续变量分离得 恒成立,即
恒成立,即 .最后只需求函数
.最后只需求函数 在
在 上最大值,就为
上最大值,就为 的最小值.(3)本题含义为:对于函数
的最小值.(3)本题含义为:对于函数 在
在 上值域中每一个值,函数
上值域中每一个值,函数 在
在 上总有两个不同自变量与之对应相等.首先求出函数
上总有两个不同自变量与之对应相等.首先求出函数 在
在 上值域
上值域 ,然后根据函数
,然后根据函数 在
在 上必须不为单调函数且每段单调区间对应的值域都需包含
上必须不为单调函数且每段单调区间对应的值域都需包含 .由
.由 在
在 不单调得
不单调得 ,由每段单调区间对应的值域都需包含
,由每段单调区间对应的值域都需包含 得
得 ,
, .
.
试题解析:(1) ,令
,令 ,得x = 1. 1分
,得x = 1. 1分
列表如下:
x | (?∞,1) | 1 | (1,∞) |
| | 0 | ? |
g(x) | ↗ | 极大值 | ↘ |
∵g(1) = 1,∴y = 的极大值为1,无极小值. 3分
的极大值为1,无极小值. 3分
(2)当 时,
时, ,
, .
.
∵ 在
在 恒成立,∴
恒成立,∴ 在
在 上为增函数. 4分
上为增函数. 4分
设 ,∵
,∵ > 0在
> 0在 恒成立,
恒成立,
∴ 在
在 上为增函数. 5分
上为增函数. 5分
设 ,则
,则 等价于
等价于 ,
,
即 .
.
设 ,则u(x)在
,则u(x)在 为减函数.
为减函数.
∴ 在(3,4)上恒成立. 6分
在(3,4)上恒成立. 6分
∴ 恒成立.设
恒成立.设 ,∵
,∵ =
= ,x?[3,4],
,x?[3,4],
∴ ,∴
,∴ < 0,
< 0, 为减函数.
为减函数.
∴ 在[3,4]上的最大值为v(3) = 3 ?
在[3,4]上的最大值为v(3) = 3 ? . 8分
. 8分
∴a≥3 ? ,∴
,∴ 的最小值为3 ?
的最小值为3 ? . 9分
. 9分
(3)由(1)知 在
在 上的值域为
上的值域为 . 10分
. 10分
∵ ,
, ,
,
当 时,
时, 在
在 为减函数,不合题意. 11分
为减函数,不合题意. 11分
当 时,
时, ,由题意知
,由题意知 在
在 不单调,
不单调,
所以 ,即
,即 .①12分
.①12分
此时 在
在 上递减,在
上递减,在 上递增,
上递增,
∴ ,即
,即 ,解得
,解得 .②
.②
由①②,得 . 13分
. 13分
∵ ,∴
,∴ 成立. 14分
成立. 14分
下证存在 ,使得
,使得 ≥1.
≥1.
取 ,先证
,先证 ,即证
,即证 .③
.③
设 ,则
,则 在
在 时恒成立.
时恒成立.
∴ 在
在 时为增函数.∴
时为增函数.∴ ,∴③成立.
,∴③成立.
再证 ≥1.
≥1.
∵ ,∴
,∴ 时,命题成立.
时,命题成立.
综上所述, 的取值范围为
的取值范围为 . 16分
. 16分
考点:函数极值,不等式恒成立


科目:高中数学 来源:2013-2014学年江苏省苏锡常镇四市高三教学情况调研二数学试卷(解析版) 题型:填空题
已知Sn为等差数列{an}的前n项和,a1 = ?1,S3 = 6,则S6 = .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省苏、锡、常、镇四市高三教学情况调查(一)理科数学试卷(解析版) 题型:解答题
甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为 ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省苏、锡、常、镇四市高三教学情况调查(一)理科数学试卷(解析版) 题型:解答题
设函数 .
.
(1)求 的最小正周期和值域;
的最小正周期和值域;
(2)在锐角△ 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 且
且 ,
, ,求
,求 和
和 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省苏、锡、常、镇四市高三教学情况调查(一)理科数学试卷(解析版) 题型:填空题
从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只有一个被选取的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com