
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() ,点
,点![]() ,
,![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 上的动点,且满足
上的动点,且满足![]() .
.
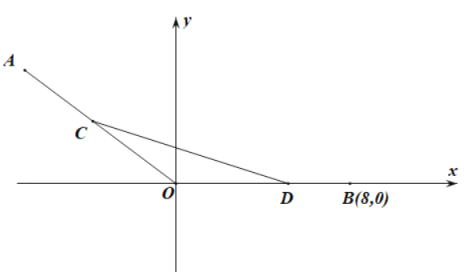
(1)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的外接圆的一般方程,并求
的外接圆的一般方程,并求![]() 的外接圆所过定点的坐标.
的外接圆所过定点的坐标.
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若两条直线与同一条直线所成的角相等,则这两条直线平行
B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行
C.若一条直线分别平行于两个相交平面,则一定平行它们的交线
D.若两个平面都平行于同一条直线,则这两个平面平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商家通常依据“乐观系数准则”确定商品销售价格,及根据商品的最低销售限价a,最高销售限价b(b>a)以及常数x(0<x<1)确定实际销售价格c=a+x(b﹣a),这里,x被称为乐观系数.
经验表明,最佳乐观系数x恰好使得(c﹣a)是(b﹣c)和(b﹣a)的等比中项,据此可得,最佳乐观系数x的值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
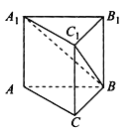
【题目】我国古代数学名著《九章算术》中有这样一些数学用语,“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,而“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.现有一如图所示的堑堵,![]() ,若
,若![]() ,当阳马
,当阳马![]() 体积最大时,则堑堵
体积最大时,则堑堵![]() 的外接球的体积为________.
的外接球的体积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学对高三年级的学生进行体质测试,已知高三、一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:![]() ):
):
|
|
| 男 |
| 女 |
|
|
|
|
|
7 | 16 | 5 | 7 | 8 | 9 | 9 | ||||
9 | 8 | 17 | 1 | 8 | 4 | 5 | 2 | 9 | ||
3 | 5 | 6 | 18 | 0 | 2 | 7 | 5 | 4 | ||
1 | 2 | 4 | 19 | 0 | 1 | |||||
1 8 5 | 20 21 22 |
男生成绩不低于![]() 的定义为“合格”,成绩低于
的定义为“合格”,成绩低于![]() 的定义为“不合格”;女生成绩不低于
的定义为“不合格”;女生成绩不低于![]() 的定义为“合格”,成绩低于
的定义为“合格”,成绩低于![]() 的定义为“不合格”.
的定义为“不合格”.
(1) 求女生立定跳远成绩的中位数;
(2) 若在男生中按成绩是否合格进行分层抽样,抽取6个人,求抽取成绩“合格”的男生人数;
(3) 若从(2)问所抽取的6人中任选2人,求这2人中恰有1人成绩“合格”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班上午有五节课,分別安排语文,数学,英语,物理,化学各一节课.要求语文与化学相邻,数学与物理不相邻,且数学课不排第一节,则不同排课法的种数是
A. 24B. 16C. 8D. 12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别相交于点B、C,经过B、C两点的抛物线
轴分别相交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一交点为A,顶点为P,且对称轴为直线
轴的另一交点为A,顶点为P,且对称轴为直线![]() .
.
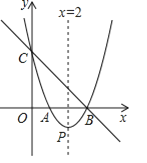
(1)求该抛物线的函数表达式;
(2)连结AC.请问在![]() 轴上是否存在点Q,使得以点P、B、Q为顶点的三角形与△ABC 相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
轴上是否存在点Q,使得以点P、B、Q为顶点的三角形与△ABC 相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知对某校的100名学生进行不记名问卷调查,内容为一周的课外阅读时长和性别等进行统计,如表:
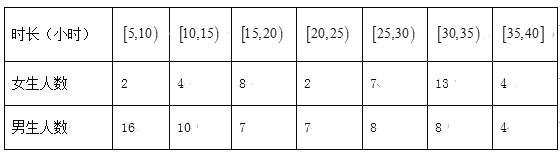
(1)课外阅读时长在20以下的女生按分层抽样的方式随机抽取7人,再从7人中随机抽取2人,求这2人课外阅读时长不低于15的概率;
(2)将课外阅读时长为25以上的学生视为“阅读爱好”者,25以下的学生视为“非阅读爱好”者,根据以上数据完成2×2列联表:
非阅读爱好者 | 阅读爱好者 | 总计 | |
女生 | |||
男生 | |||
总计 |
能否在犯错概率不超过0.01的前提下,认为学生的“阅读爱好”与性别有关系?
附:![]() ,
,
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com