
分析 (1)求出f(x)解析式并利用三角函数恒等变换化简,列出方程解出,
(2)利用函数的图象变换规律写出g(x)的解析式,结合余弦函数的性质列不等式解出.
解答 解:(1)f(x)=-2sinxcosx+2sin(x+$\frac{π}{2}$)cosx+1=2cos2x-sin2x+1=cos2x-sin2x+2=$\sqrt{2}$cos(2x+$\frac{π}{4}$)+2.
∵f(x)-1=0,∴cos(2x+$\frac{π}{4}$)=-$\frac{\sqrt{2}}{2}$,∵x∈(0,π),∴x1=$\frac{π}{4}$,x2=$\frac{π}{2}$,
∴f(x1+x2)=f($\frac{3π}{4}$)=$\sqrt{2}$cos$\frac{7π}{4}$+2=3.
(2)g(x)=$\sqrt{2}$cos([2(x+$\frac{π}{3}$)+$\frac{π}{4}$]+2+2=$\sqrt{2}$cos(2x+$\frac{11π}{12}$)+4.
则g(x)的单调递增区间:令-π+2kπ≤2x+$\frac{11π}{12}$≤2kπ,解得kπ-$\frac{23π}{24}$≤x≤kπ-$\frac{11π}{24}$,
∴函数g(x)的单调增区间是[kπ-$\frac{23π}{24}$,kπ-$\frac{11π}{24}$],k∈Z.
点评 本题考查了平面向量与三角函数的综合,三角函数恒等变换,属于中档题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:选择题
| A. | x1+x2=2 | B. | 9<x3•x4<25 | C. | 0<(6-x3)•(6-x4)<1 | D. | 1<x1•x2<9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
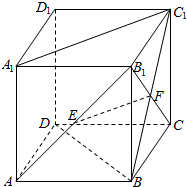
| A. | EF与BB1垂直 | B. | EF与BD垂直 | C. | EF与CD异面 | D. | EF与A1C1异面 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
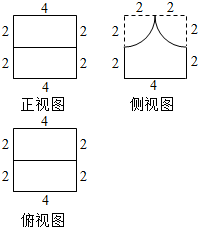 某几何体的三视图如图所示(其中侧视图为正方形上半部分在两个角上各截去四分之一圆),则该几何体的表面积为( )
某几何体的三视图如图所示(其中侧视图为正方形上半部分在两个角上各截去四分之一圆),则该几何体的表面积为( )| A. | 48+4π | B. | 48+8π | C. | 64+4π | D. | 64+8π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “b2=ac”是“a,b,c成等比数列”的充要条件 | |
| B. | “?x∈R,x2>0”的否定是“?x0∈R,x02>0” | |
| C. | “若a=-4,则函数f(x)=ax2+4x-1只有唯一一个零点”的逆命题为真命题 | |
| D. | “函数f(x)=lnx2与函数g(x)=$\left\{\begin{array}{l}{2lnx,x>0}\\{2ln(-x),x<0}\end{array}\right.$的图象相同” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com