
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,且(a+b+c)(a+b﹣c)=3ab.
(Ⅰ)求角C的值;
(Ⅱ)若c=2,且△ABC为锐角三角形,求a+b的取值范围.
【答案】解:(Ⅰ)△ABC中,(a+b+c)(a+b﹣c)=3ab,
∴a2+b2﹣c2=ab,
由余弦定理得,cosC= ![]() =
= ![]() ;
;
又∵C∈(0,π),
∴C= ![]() ;
;
(Ⅱ)由c=2,C= ![]() ,根据正弦定理得,
,根据正弦定理得,
![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴a+b= ![]() (sinA+sinB)
(sinA+sinB)
= ![]() [sinA+sin(
[sinA+sin( ![]() ﹣A)]
﹣A)]
=2 ![]() sinA+2cosA
sinA+2cosA
=4sin(A+ ![]() );
);
又∵△ABC为锐角三角形,
∴ 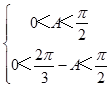 ,
,
解得 ![]() <A<
<A< ![]() ;
;
∴ ![]() <A+
<A+ ![]() <
< ![]() ,
,
∴2 ![]() <4sin(A+
<4sin(A+ ![]() )≤4,
)≤4,
综上,a+b的取值范围是(2 ![]() ,4]
,4]
【解析】(Ⅰ)化简(a+b+c)(a+b﹣c)=3ab,利用余弦定理求得C的值;(Ⅱ)由正弦定理求出a+b的解析式,利用三角恒等变换化简,根据题意求出A的取值范围,从而求出a+b的取值范围.
【考点精析】根据题目的已知条件,利用余弦定理的定义的相关知识可以得到问题的答案,需要掌握余弦定理:![]() ;
;![]() ;
;![]() .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() mcos2x+(m﹣2)sinx,其中1≤m≤2,若函数f(x)的最大值记为g(m),则g(m)的最小值为( )
mcos2x+(m﹣2)sinx,其中1≤m≤2,若函数f(x)的最大值记为g(m),则g(m)的最小值为( )
A.﹣ ![]()
B.1
C.3﹣ ![]()
D.![]() ﹣1
﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为  (其中t为参数),现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=4cosθ.
(其中t为参数),现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=4cosθ.
(Ⅰ)写出直线l和曲线C的普通方程;
(Ⅱ)已知点P为曲线C上的动点,求P到直线l的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A,ω,φ均为正的常数)的最小正周期为π,当x= ![]() 时,函数f(x)取得最小值,则下列结论正确的是( )
时,函数f(x)取得最小值,则下列结论正确的是( )
A.f(2)<f(﹣2)<f(0)
B.f(0)<f(2)<f(﹣2)
C.f(﹣2)<f(0)<f(2)
D.f(2)<f(0)<f(﹣2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明1+2+3+…+n2= ![]() ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
A.k2+1
B.(k+1)2
C.![]()
D.(k2+1)+(k2+2)+(k2+3)+…+(k+1)2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 ![]() (0≤α<π,t为参数),曲线C的极坐标方程为ρ=
(0≤α<π,t为参数),曲线C的极坐标方程为ρ= ![]() .
.
(Ⅰ)将曲线C的极坐标方程化为直角坐标方程,并说明曲线C的形状;
(Ⅱ)若直线l经过点(1,0),求直线l被曲线C截得的线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C. 
(Ⅰ)证明:AC=AB1;
(Ⅱ)若AC⊥AB1 , ∠CBB1=60°,AB=BC,求二面角A﹣A1B1﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某产品的广告费用x(单位:万元)与销售额y(单位:万元)具有线性关系关系,其统计数据如下表:
x | 3 | 4 | 5 | 6 |
y | 25 | 30 | 40 | 45 |
由上表可得线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,据此模型预报广告费用为8万元时的销售额是( )
,据此模型预报广告费用为8万元时的销售额是( )
附: ![]() =
= 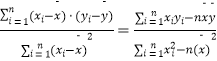 ;
; ![]() =
= ![]() ﹣
﹣ ![]() x.
x.
A.59.5
B.52.5
C.56
D.63.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(Ⅰ)求CE与DB所成角的余弦值;
(Ⅱ)设点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长度
的长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com