
【题目】如图,AB为⊙O的直径,点C在⊙O上,且∠AOC=120°,PA⊥平面ABC,AB=4,PA=2![]() ,D是PC的中点,点M是⊙O上的动点(不与A,C重合).
,D是PC的中点,点M是⊙O上的动点(不与A,C重合).
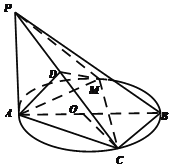
(1)证明:AD⊥PB;
(2)当三棱锥D﹣ACM体积最大时,求面MAD与面MCD所成二面角的正弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据题意可证![]() ,
,![]() ,即可证明
,即可证明![]() 平面
平面![]() ,从而证得:
,从而证得:![]() ;
;
(2)以E为原点,分别以EC,EM,ED为x轴、y轴和z轴,表示出各点坐标,求出平面MAD的法向量与平面MCD的法向量,利用二面角公式即可得到答案。
(1)证明:∵![]() 为圆
为圆![]() 的直径,∴
的直径,∴![]() ,∵
,∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,又
,又![]() ,∴
,∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() ,又
,又![]() ,
,
∴![]() ,又
,又![]() 是
是![]() 的中点,∴
的中点,∴![]() ,又
,又![]() ,∴
,∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴![]() .
.
(2)当三棱锥D﹣ACM体积最大时,三角形ACM的面积最大,取AC的中点E,M点为EO延长线与圆O的交点.
∴DE∥AP,EM⊥AC,以E为原点,分别以EC,EM,ED为x轴、y轴和z轴,建立如图所示空间直角坐标系.
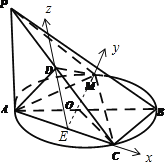
又∵MA=MC=AC=![]() ,DE=
,DE=![]() PA=
PA=![]() ,ME=3.
,ME=3.
∴M(0,3,0),D(0,0,![]() ),A(﹣
),A(﹣![]() ,0,0),C(
,0,0),C(![]() ,0,0),
,0,0),
∴![]() ,
,![]() ,
,![]() ,
,
设平面MAD的法向量为![]() ,则
,则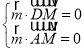 ,即
,即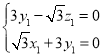 ,
,
令![]() 可得
可得![]() ,
,
设平面MCD的法向量为![]() ,则
,则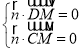 ,即
,即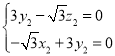 ,
,
令![]() 可得
可得![]() ,设面MAD与面MCD所成二面角为
,设面MAD与面MCD所成二面角为![]() ,则
,则
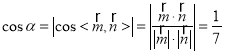 ,∴
,∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点
为参数),以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程是:
的极坐标方程是:![]()
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程.
的直角坐标方程.
(2)点![]() 是曲线
是曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 距离的最大值与最小值.
距离的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018 年1月16日,由新华网和中国财经领袖联盟联合主办的2017中国财经年度人物评选结果揭晓,某知名网站财经频道为了解公众对这些年度人物是否了解,利用网络平台进行了调查,并从参与调查者中随机选出![]() 人,把这
人,把这![]() 人分为
人分为![]() 两类(
两类(![]() 类表示对这些年度人物比较了解,
类表示对这些年度人物比较了解,![]() 类表示对这些年度人物不太了解),并制成如下表格:
类表示对这些年度人物不太了解),并制成如下表格:
年龄段 |
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
(1)若按照年龄段进行分层抽样,从这![]() 人中选出
人中选出![]() 人进行访谈,并从这
人进行访谈,并从这![]() 人中随机选出两名幸运者给予奖励.求其中一名幸运者的年龄在
人中随机选出两名幸运者给予奖励.求其中一名幸运者的年龄在![]() 岁~
岁~![]() 岁之间,另一名幸运者的年龄在
岁之间,另一名幸运者的年龄在![]() 岁~
岁~![]() 岁之间的概率;(注:从
岁之间的概率;(注:从![]() 人中随机选出
人中随机选出![]() 人,共有
人,共有![]() 种不同选法)
种不同选法)
(2)如果把年龄在![]() 岁~
岁~![]() 岁之间的人称为青少年,年龄在
岁之间的人称为青少年,年龄在![]() 岁~
岁~![]() 岁之间的人称为中老年,则能否在犯错误的概率不超过
岁之间的人称为中老年,则能否在犯错误的概率不超过![]() 的前提下认为青少年与中老年人在对财经年度人物的了解程度上有差异?
的前提下认为青少年与中老年人在对财经年度人物的了解程度上有差异?
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着城市地铁建设的持续推进,市民的出行也越来越便利.根据大数据统计,某条地铁线路运行时,发车时间间隔t(单位:分钟)满足:4≤t≤15,![]() N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系:
N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系: ,其中
,其中![]() .
.
(1)若平均每趟地铁的载客人数不超过1500人,试求发车时间间隔t的值.
(2)若平均每趟地铁每分钟的净收益为![]() (单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
(单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,椭圆
,椭圆![]() 上任意一点到椭圆两个焦点的距离之和为6.
上任意一点到椭圆两个焦点的距离之和为6.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]()
![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() (0,1),且
(0,1),且![]() =
=![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣2)ex﹣![]() +
+![]() x,其中
x,其中![]() ∈R,e是自然对数的底数.
∈R,e是自然对数的底数.
(1)当![]() >0时,讨论函数f(x)在(1,+∞)上的单调性;
>0时,讨论函数f(x)在(1,+∞)上的单调性;
(2)若函数g(x)=f![]() (x)+2﹣
(x)+2﹣![]() ,证明:使g(x)≥0在
,证明:使g(x)≥0在![]() 上恒成立的实数a能取到的最大整数值为1.
上恒成立的实数a能取到的最大整数值为1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的各项都是正数,若对于任意的正整数
的各项都是正数,若对于任意的正整数![]() ,存在
,存在![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列,则称函数
成等比数列,则称函数![]() 为“
为“![]() 型”数列.
型”数列.
(1)若![]() 是“
是“![]() 型”数列,且
型”数列,且![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)若![]() 是“
是“![]() 型”数列,且
型”数列,且![]() ,
,![]() ,求
,求![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]() 既是“
既是“![]() 型”数列,又是“
型”数列,又是“![]() 型”数列,求证:数列
型”数列,求证:数列![]() 是等比数列.
是等比数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com