
分析 (1)(2)消去参数,可化参数方程为普通方程;
(3)由(1)(2)可知P到C2的距离为$d=\frac{{|2cosθ+2\sqrt{3}sinθ-4|}}{{\sqrt{5}}}=\frac{{|4sin(θ+\frac{π}{6})-4|}}{{\sqrt{5}}}$,即可得出结论.
解答 解:(1)当t=0时,原方程即为$\left\{{\begin{array}{l}x=2cosθ\\ y=\sqrt{3}sinθ\end{array}}\right.$,消参得${C_1}:\frac{x^2}{4}+\frac{y^2}{3}=1$.…(3分)
(2)当$θ=\frac{π}{3}$.原方程即为$\left\{{\begin{array}{l}x=-\frac{{2\sqrt{5}}}{5}t+1\\ y=\frac{{\sqrt{5}}}{5}t+\frac{3}{2}\end{array}}\right.$,消参得C2:x+2y-4=0…(6分)
(3)由(1)(2)可知P到C2的距离为$d=\frac{{|2cosθ+2\sqrt{3}sinθ-4|}}{{\sqrt{5}}}=\frac{{|4sin(θ+\frac{π}{6})-4|}}{{\sqrt{5}}}$
当$sin(θ+\frac{π}{6})=-1$时,${d_{max}}=\frac{{8\sqrt{5}}}{5}$…(10分)
点评 本题考查参数方程化为普通方程,考查点到直线距离公式的运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
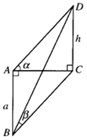 一个建筑物CD垂直于水平面,一个人在建筑物的正西A点,测得建筑物顶端的仰角是α,这个人再从A点向南走到B点,再测得建筑物顶端仰角是β,设A、B两地距离为a,求建筑物的高h的值(A,B,C三点在同一水平面内).
一个建筑物CD垂直于水平面,一个人在建筑物的正西A点,测得建筑物顶端的仰角是α,这个人再从A点向南走到B点,再测得建筑物顶端仰角是β,设A、B两地距离为a,求建筑物的高h的值(A,B,C三点在同一水平面内).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{4\sqrt{2}}}{9}$ | B. | $\frac{{4\sqrt{2}}}{9}$ | C. | $-\frac{7}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 110 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com