
如图,在五面体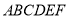 中,四边形
中,四边形 是边长为
是边长为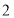 的正方形,
的正方形,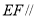 平面
平面 ,
,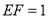 ,
,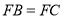 ,
,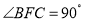 ,
,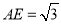 .
.
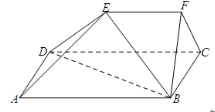
(1)求证: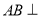 平面
平面 ;
;
(2)求直线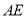 与平面
与平面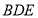 所成角的正切值.
所成角的正切值.
(1)详见解析;(2) .
.
【解析】
试题分析:(1)取 的中点
的中点 ,先证明四边形
,先证明四边形 为平行四边形得到
为平行四边形得到 ,然后通过勾股定理证明
,然后通过勾股定理证明 从而得到
从而得到 ,然后结合四边形
,然后结合四边形 为正方形得到
为正方形得到 ,最后利用直线与平面垂直的判定定理证明
,最后利用直线与平面垂直的判定定理证明 平面
平面 ;(2)解法1是先取
;(2)解法1是先取 的中点
的中点 ,连接
,连接 ,利用(1)中的结论
,利用(1)中的结论 平面
平面 得到
得到 ,利用等腰三角形
,利用等腰三角形 三线合一得到
三线合一得到 ,利用直线与平面垂直的判定定理得到
,利用直线与平面垂直的判定定理得到 平面
平面 ,通过证明四边形
,通过证明四边形 为平行四边形得到
为平行四边形得到 ,从而得到
,从而得到 平面
平面 ,从而得到
,从而得到 ,然后利用底面四边形
,然后利用底面四边形 为正方形得到
为正方形得到 ,由这两个条件来证明
,由这两个条件来证明 平面
平面 ,从而得到
,从而得到 是直线
是直线 与平面
与平面 所成的角,然后在直角
所成的角,然后在直角 中计算
中计算 ,从而求出直线
,从而求出直线 与平面
与平面 所成角的正切值;解法2是先取
所成角的正切值;解法2是先取 的中点
的中点 ,连接
,连接 ,利用(1)中的结论
,利用(1)中的结论 平面
平面 得到
得到 ,利用等腰三角形
,利用等腰三角形 三线合一得到
三线合一得到 ,利用直线与平面垂直的判定定理得到
,利用直线与平面垂直的判定定理得到 平面
平面 ,然后选择以
,然后选择以 为坐标原点,
为坐标原点, 所在直线为
所在直线为 轴,
轴, 所在直线为
所在直线为 轴,
轴, 所在直线为
所在直线为 轴,建立空间直角坐标系
轴,建立空间直角坐标系 ,利用空间向量法结合同角三角函数的基本关系求出线
,利用空间向量法结合同角三角函数的基本关系求出线 与平面
与平面 所成角的正切值.
所成角的正切值.
试题解析:(1)取 的中点
的中点 ,连接
,连接 ,则
,则 ,
,

由(1)知, ,且
,且 ,
, 四边形
四边形 为平行四边形,
为平行四边形,
 ,
, ,
,
在 中,
中, ,又
,又 ,得
,得 ,
, ,
,
在 中,
中, ,
, ,
, ,
,
 ,
, ,
, ,即
,即 ,
,
 四边形
四边形 是正方形,
是正方形, ,
,
 ,
, 平面
平面 ,
, 平面
平面 ,
, 平面
平面 ;
;
(2)解法1:连接 ,
, 与
与 相交于点
相交于点 ,则点
,则点 是
是 的中点,
的中点,
取 的中点
的中点 ,连接
,连接 、
、 、
、 ,
,

则 ,
, .
.
由(1)知 ,且
,且 ,
, ,且
,且 .
.
 四边形
四边形 是平行四边形.
是平行四边形.
 ,且
,且 ,
,
由(1)知 平面
平面 ,又
,又 平面
平面 ,
, .
.
 ,
, ,
, 平面
平面 ,
, 平面
平面 ,
,
 平面
平面 .
. 平面
平面 .
.
 平面
平面 ,
, .
.
 ,
, ,
, 平面
平面 ,
, 平面
平面 ,
, 平面
平面 .
.
 是直线
是直线 与平面
与平面 所成的角.
所成的角.
在 中,
中, .
.
 直线
直线 与平面
与平面 所成角的正切值为
所成角的正切值为 ;
;
解法2:连接 ,
, 与
与 相交于点
相交于点 ,则点
,则点 是
是 的中点,
的中点,
则 ,
, .由(1)知
.由(1)知 ,且
,且 ,
, ,且
,且 .
.
 四边形
四边形 是平行四边形.
是平行四边形.

 ,且
,且 ,
,
由(1)知 平面
平面 ,又
,又 平面
平面 ,
, .
.
 ,
, ,
, 平面
平面 ,
, 平面
平面 ,
,
 平面
平面 .
. 平面
平面 .
.
以 为坐标原点,
为坐标原点, 所在直线为
所在直线为 轴,
轴, 所在直线为
所在直线为 轴,
轴, 所在直线为
所在直线为 轴,
轴,
建立空间直角坐标系 ,则
,则 ,
, ,
, ,
, .
.

 ,
, ,
, .
.
设平面 的法向量为
的法向量为 ,由
,由 ,
, ,
,
得 ,
, ,得
,得 .
.
令 ,则平面
,则平面 的一个法向量为
的一个法向量为 .
.
设直线 与平面
与平面 所成角为
所成角为 ,
,
则 .
. ,
, .
.
 直线
直线 与平面
与平面 所成角的正切值为
所成角的正切值为 .
.
考点:1.直线与平面垂直;2.直线与平面所成的角;3.空间向量法


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2013-2014学年广东省揭阳市高三4月第二次模拟考试文科数学试卷(解析版) 题型:选择题
下列函数中,既是偶函数又在区间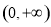 上存在零点的是( )
上存在零点的是( )
A. B.
B.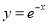 C.
C.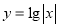 D.
D.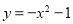
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省揭阳市高三3月第一次模拟考试文科数学试卷(解析版) 题型:选择题
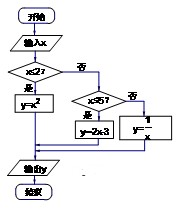
如图所示的程序框图,能使输入的 值与输出的
值与输出的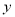 值相等的
值相等的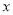 值分别为( )
值分别为( )
A.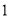 、
、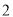 、
、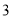 B.
B.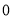 、
、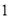 C.
C.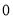 、
、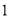 、
、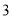 D.
D.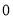 、
、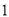 、
、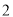 、
、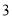 、
、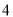
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省广州市毕业班综合测试二理科数学试卷(解析版) 题型:填空题
已知 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如 ,
, .设函数
.设函数 ,当
,当 时,函数
时,函数 的值域为集合
的值域为集合 ,则
,则 中的元素个数为.
中的元素个数为.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省广州市毕业班综合测试二理科数学试卷(解析版) 题型:选择题
设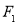 、
、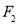 分别是椭圆
分别是椭圆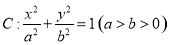 的左、右焦点,点
的左、右焦点,点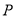 在椭圆
在椭圆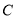 上,线段
上,线段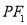 的中点在
的中点在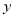 轴上,若
轴上,若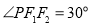 ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A.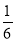 B.
B. C.
C.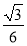 D.
D.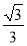
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省广州市毕业班综合测试二文科数学试卷(解析版) 题型:选择题
将正偶数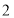 、
、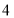 、
、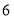 、
、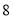 、
、 按表
按表 的方式进行排列,记
的方式进行排列,记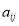 表示第
表示第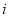 行和第
行和第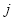 列的数,若
列的数,若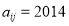 ,则
,则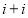 的值为( )
的值为( )
| 第 | 第 | 第 | 第 | 第 |
第 |
|
|
|
|
|
第 |
|
|
|
|
|
第 |
|
|
|
|
|
第 |
|
|
|
|
|
第 |
|
|
|
|
|
|
|
|
|
|
|
A.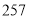 B.
B.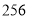 C.
C.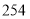 D.
D.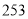
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com