
【题目】如图所示,正三棱柱![]() 的高为2,
的高为2,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点
的中点
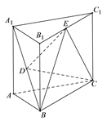
(1)证明:![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积为
的体积为![]() ,求该正三棱柱的底面边长.
,求该正三棱柱的底面边长.
【答案】(1)见解析(2)2
【解析】
试题分析:(1)由三角形中位线性质得DE//AC1,再根据线面平行判定定理得结果(2)根据平行性质得D到平面BCC1B1的距离是A到平面BCC1B1的距离的一半,再根据锥体体积公式列方程解得底面边长
试题解析:(Ⅰ)证明:如图,连接AB1,AC1,
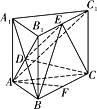
易知D是AB1的中点,
又E是B1C1的中点,
所以在![]() 中,DE//AC1,
中,DE//AC1,
又DE![]() 平面ACC1A1,AC1
平面ACC1A1,AC1![]() 平面ACC1A1,
平面ACC1A1,
所以DE//平面ACC1A1.
(Ⅱ)解:![]() ,
,
![]() D是AB1的中点,
D是AB1的中点,
![]() D到平面BCC1B1的距离是A到平面BCC1B1的距离的一半,
D到平面BCC1B1的距离是A到平面BCC1B1的距离的一半,
如图,作AF![]() BC交BC于F,由正三棱柱的性质,易证AF
BC交BC于F,由正三棱柱的性质,易证AF![]() 平面BCC1B1,
平面BCC1B1,
设底面正三角形边长为![]() ,则三棱锥DEBC的高h=
,则三棱锥DEBC的高h=![]() AF=
AF=![]() ,
,
![]() ,所以
,所以![]() ,
,
解得![]() .
.
所以该正三棱柱的底面边长为2.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线l的参数方程为  (t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为:ρ2﹣3ρ﹣4=0(ρ≥0).
(t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为:ρ2﹣3ρ﹣4=0(ρ≥0).
(1)写出直线l的普通方程与曲线C的直角坐标系方程;
(2)设直线l与曲线C相交于A,B两点,求∠AOB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a、b、c为三条不重合的直线,α、β、γ为三个不重合的平面,现给出六个命题.
①![]() a∥b; ②
a∥b; ②![]() a∥b; ③
a∥b; ③![]() α∥β;
α∥β;
④![]() α∥β; ⑤
α∥β; ⑤![]() a∥α; ⑥
a∥α; ⑥![]() a∥α,
a∥α,
其中正确的命题是________.(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】不等式|x﹣ ![]() ≤
≤ ![]() 的解集为{x|n≤x≤m}
的解集为{x|n≤x≤m}
(1)求实数m,n;
(2)若实数a,b满足:|a+b|<m,|2a﹣b|<n,求证:|b|< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆相交于
与椭圆相交于![]() ,
, ![]() 两点,
两点, ![]() ,
, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点,若坐标原点
的中点,若坐标原点![]() 在以
在以![]() 为直径的圆上,求
为直径的圆上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设首项为1的正项数列{an}的前n项和为Sn , 且Sn+1﹣3Sn=1.
(1)求证:数列{an}为等比数列;
(2)数列{an}是否存在一项ak , 使得ak恰好可以表示为该数列中连续r(r∈N* , r≥2)项的和?请说明理由;
(3)设 ![]() ,试问是否存在正整数p,q(1<p<q)使b1 , bp , bq成等差数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
,试问是否存在正整数p,q(1<p<q)使b1 , bp , bq成等差数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com