
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若存在实数![]() ,使
,使![]() ,求实数
,求实数![]() 的范围.
的范围.
【答案】(1)答案不唯一,具体见解析(2)![]()
【解析】
(1)求导,分类讨论即可求得单调性情况;(2)分a=0,a<0及a>0三种情况讨论即可求得实数a的取值范围.
(1)函数![]() 的导函数为
的导函数为![]() ,
,
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)当![]() 时,
时,![]() ,有
,有![]() ,不符合题意;
,不符合题意;
当![]() 时,由(1)知
时,由(1)知![]() ,
,
由![]() 在
在![]() 单调递增,且
单调递增,且![]() 知,
知,
①当![]() 时,由(1)知
时,由(1)知![]() ,
,
此时![]() 恒成立,不符合题意;
恒成立,不符合题意;
②当![]() 时,
时,![]() ,
,
(预备:很容易证明![]() ,而
,而![]() ,
,
所以,![]() ,即
,即![]() ,
,
所以,![]() .)
.)
由![]() ,
,
有![]() ,即
,即![]() .
.
所以存在![]() ,使得
,使得![]() 满足题意.
满足题意.
当![]() 时,由(1)知
时,由(1)知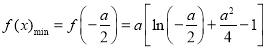 ,
,
由![]() 在
在![]() 上单调递减,且
上单调递减,且![]() 知,
知,
当![]() 时,
时,![]() 恒成立,不满足题意;
恒成立,不满足题意;
当![]() 时,
时,![]() ,
,
(预备:很容易证明![]() ,而
,而![]() ,
,
所以,![]() ,即
,即![]() ,
,
所以,![]() .)
.)
由![]() ,
,
有![]() ,即
,即![]() ,
,
所以存在![]() ,使得
,使得![]() 满足题意.
满足题意.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 与
与![]() 的图象关于点
的图象关于点![]() 对称.
对称.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() 有两个不同零点,求实数
有两个不同零点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上是单调减函数,求实数
上是单调减函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(3)在(2)的条件下,设函数![]() ,若对于
,若对于![]() ,
,![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
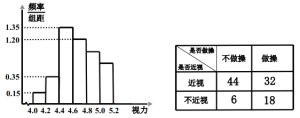
【题目】眼保健操是一种眼睛的保健体操,主要是通过按摩眼部穴位,调整眼及头部的血液循环,调节肌肉,改善眼的疲劳,达到预防近视等眼部疾病的目的.某学校为了调查推广眼保健操对改善学生视力的效果,在应届高三的全体800名学生中随机抽取了100名学生进行视力检查,并得到如图的频率分布直方图.
(1)若直方图中后三组的频数成等差数列,试估计全年级视力在5.0以上的人数;
(2)为了研究学生的视力与眼保健操是否有关系,对年级不做眼保健操和坚持做眼保健操的学生进行了调查,得到下表中数据,根据表中的数据,能否在犯错的概率不超过0.005的前提下认为视力与眼保健操有关系?
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取8人,进一步调查他们良好的护眼习惯,在这8人中任取2人,记坚持做眼保健操的学生人数为X,求X的分布列和数学期望.
附: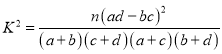
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某厂的某种产品400件,经质检,其中有一等品252件、二等品100件、三等品40件、次品8件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为![]() .
.
(1)求![]() 的分布列和1件产品的平均利润(即
的分布列和1件产品的平均利润(即![]() 的期望);
的期望);
(2)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求1件产品的平均利润不小于4.75万元,则三等品率最多是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司新发明了甲、乙两种不同型号的手机,公司统计了消费者对这两种型号手机的评分情况,作出如下的雷达图,则下列说法不正确的是( )

A. 甲型号手机在外观方面比较好.B. 甲、乙两型号的系统评分相同.
C. 甲型号手机在性能方面比较好.D. 乙型号手机在拍照方面比较好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,M在线段
,M在线段![]() 上,且
上,且![]() .
.
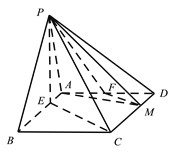
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)在线段AD上确定一点F,使得平面![]() 平面PAB,并求三棱锥
平面PAB,并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com